完美解决Tensorflow不支持AVX2指令集问题|指令集加速
在pycharm中安装tensorflow后
在pycharm中安装tensorflow后
Classification
1 | # To support both python 2 and python 3 |
首先定义一个向量为:x=[-5,6,8, -10]
1-范数:
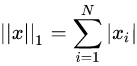 ,即向量的各个元素的绝对值之和,matlab调用函数norm(x, 1) 。则上述x的1-范数结果是29
,即向量的各个元素的绝对值之和,matlab调用函数norm(x, 1) 。则上述x的1-范数结果是29
2-范数:
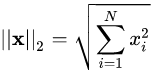 ,Euclid范数(欧几里得范数,常用计算向量长度),即向量元素绝对值的平方和再开方,matlab调用函数norm(x, 2)。
,Euclid范数(欧几里得范数,常用计算向量长度),即向量元素绝对值的平方和再开方,matlab调用函数norm(x, 2)。
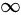 -范数:
-范数:
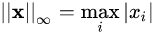 ,即所有向量元素绝对值中的最大值,matlab调用函数norm(x, inf)。
,即所有向量元素绝对值中的最大值,matlab调用函数norm(x, inf)。
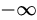 -范数:
-范数:
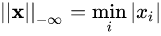 ,即所有向量元素绝对值中的最小值,matlab调用函数norm(x, -inf)。
,即所有向量元素绝对值中的最小值,matlab调用函数norm(x, -inf)。
p-范数:
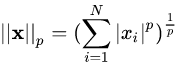 ,即向量元素绝对值的p次方和的1/p次幂,matlab调用函数norm(x, p)。
,即向量元素绝对值的p次方和的1/p次幂,matlab调用函数norm(x, p)。
矩阵的1范数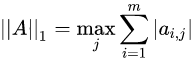 列和范数,即所有矩阵列向量绝对值之和的最大值,矩阵的每一列上的元素绝对值先求和,再从中取个最大的(列和最大)。matlab调用函数norm(A, 1)。
列和范数,即所有矩阵列向量绝对值之和的最大值,矩阵的每一列上的元素绝对值先求和,再从中取个最大的(列和最大)。matlab调用函数norm(A, 1)。
矩阵的2范数:
矩阵的2范数即:矩阵$A^{T} A$的最大特征值开平方根。
矩阵的无穷范数:
矩阵的每一行上的元素绝对值先求和,再从中取个最大的(行和最大)
L0范数是指向量中非零元素的个数。如果用L0规则化一个参数矩阵W,就是希望W中大部分元素是零,实现稀疏。
L1范数是指向量中各个元素的绝对值之和,也叫”系数规则算子(Lasso regularization)“。L1范数也可以实现稀疏,通过将无用特征对应的参数W置为零实现。
L0和L1都可以实现稀疏化,不过一般选用L1而不用L0,原因包括:1)L0范数很难优化求解(NP难);2)L1是L0的最优凸近似,比L0更容易优化求解。(这一段解释过于数学化,姑且当做结论记住)
稀疏化的好处是是什么?
1)特征选择
实现特征的自动选择,去除无用特征。稀疏化可以去掉这些无用特征,将特征对应的权重置为零。
2)可解释性(interpretability)
例如判断某种病的患病率时,最初有1000个特征,建模后参数经过稀疏化,最终只有5个特征的参数是非零的,那么就可以说影响患病率的主要就是这5个特征。
L2范数是指向量各元素的平方和然后开方,用在回归模型中也称为岭回归(Ridge regression)。
L2避免过拟合的原理是:让L2范数的规则项||W||2 尽可能小,可以使得W每个元素都很小,接近于零,但是与L1不同的是,不会等于0;这样得到的模型抗干扰能力强,参数很小时,即使样本数据x发生很大的变化,模型预测值y的变化也会很有限。
参考链接:https://www.cnblogs.com/MengYan-LongYou/p/4050862.html
https://blog.csdn.net/Michael__Corleone/article/details/75213123
### 任务介绍:
在自然语言处理中,情感分析一般指判断一段文本所表达的情绪状态,属于文本分类问题。
情绪:正面/负面IMDB数据集包含来自互联网的50000条严重两极分化的评论,该数据被分为用于训练的25000条评论和用于测试的25000条评论,训练集和测试集都包含50%的正面评价和50%的负面评价。该数据集已经经过预处理:评论(单词序列)已经被转换为整数序列,其中每个整数代表字典中的某个单词。创建数据读取器train_reader 和test_reader
定义网络
定义损失函数
定义优化算法
1 | # 导入必要的包 |
1 | !mkdir -p /home/aistudio/.cache/paddle/dataset/imdb/ |
1 | # 获取数据字典 |
加载数据字典中...
完成数据是以数据标签的方式表示一个句子。
所以每个句子都是以一串整数来表示的,每个数字都是对应一个单词。
数据集就会有一个数据集字典,这个字典是训练数据中出现单词对应的数字标签。
1 | # 获取训练和预测数据 |
加载训练数据中...
加载测试数据中...
完成1 | # 定义长短期记忆网络 |
这里可以先定义一个输入层,这样要注意的是我们使用的数据属于序列数据,所以我们可以设置lod_level为1,当该参数不为0时,表示输入的数据为序列数据,默认lod_level的值是0.
1 | # 定义输入数据, lod_level不为0指定输入数据为序列数据 |
接着定义损失函数,这里同样是一个分类任务,所以使用的损失函数也是交叉熵损失函数。这里也可以使用fluid.layers.accuracy()接口定义一个输出分类准确率的函数,可以方便在训练的时候,输出测试时的分类准确率,观察模型收敛的情况。
1 | # 获取损失函数和准确率 |
1 | # 获取预测程序 |
然后是定义优化方法,这里使用的时Adagrad优化方法,Adagrad优化方法多用于处理稀疏数据,设置学习率为0.002。
1 | # 定义优化方法 |
如果读取有GPU环境,可以尝试使用GPU来训练,使用方式是使用fluid.CUDAPlace(0)来创建。
1 | # 定义使用CPU还是GPU,使用CPU时use_cuda = False,使用GPU时use_cuda = True |
[]定义数据数据的维度,数据的顺序是一条句子数据对应一个标签。
1 | # 定义输入数据的维度 |
现在就可以开始训练了,这里设置训练的循环是2次,大家可以根据情况设置更多的训练轮数。我们在训练中,每40个Batch打印一层训练信息和进行一次测试,测试是使用测试集进行预测并输出损失值和准确率,测试完成之后,对之前预测的结果进行求平均值。
1 | # 开始训练 |
Pass:0, Batch:0, Cost:0.73125
Pass:0, Batch:40, Cost:0.06795
Pass:0, Batch:80, Cost:0.00722
Pass:0, Batch:120, Cost:0.80844
Pass:0, Batch:160, Cost:0.22205
Test:0, Cost:1.12195, ACC:0.50171
Pass:1, Batch:0, Cost:2.13347
Pass:1, Batch:40, Cost:0.48804
Pass:1, Batch:80, Cost:0.21535
Pass:1, Batch:120, Cost:0.81571
Pass:1, Batch:160, Cost:0.33186
Test:1, Cost:0.83362, ACC:0.50191
Pass:2, Batch:0, Cost:1.40742
Pass:2, Batch:40, Cost:0.55047
Pass:2, Batch:80, Cost:0.27269
Pass:2, Batch:120, Cost:0.74456
Pass:2, Batch:160, Cost:0.35957
Test:2, Cost:0.71608, ACC:0.50769
Pass:3, Batch:0, Cost:1.12344
Pass:3, Batch:40, Cost:0.55675
Pass:3, Batch:80, Cost:0.30137
Pass:3, Batch:120, Cost:0.67230
Pass:3, Batch:160, Cost:0.35690
Test:3, Cost:0.63739, ACC:0.54560
Pass:4, Batch:0, Cost:0.98897
Pass:4, Batch:40, Cost:0.55052
Pass:4, Batch:80, Cost:0.29672
Pass:4, Batch:120, Cost:0.59823
Pass:4, Batch:160, Cost:0.35738
Test:4, Cost:0.57975, ACC:0.61902
Pass:5, Batch:0, Cost:0.80312
Pass:5, Batch:40, Cost:0.50581
Pass:5, Batch:80, Cost:0.27092
Pass:5, Batch:120, Cost:0.55160
Pass:5, Batch:160, Cost:0.32211
Test:5, Cost:0.53265, ACC:0.69416
Pass:6, Batch:0, Cost:0.70552
Pass:6, Batch:40, Cost:0.49984
Pass:6, Batch:80, Cost:0.27171
Pass:6, Batch:120, Cost:0.52073
Pass:6, Batch:160, Cost:0.31178
Test:6, Cost:0.49651, ACC:0.74736
Pass:7, Batch:0, Cost:0.69794
Pass:7, Batch:40, Cost:0.50185
Pass:7, Batch:80, Cost:0.27300
Pass:7, Batch:120, Cost:0.46273
Pass:7, Batch:160, Cost:0.35845
Test:7, Cost:0.46813, ACC:0.78116
Pass:8, Batch:0, Cost:0.61882
Pass:8, Batch:40, Cost:0.45831
Pass:8, Batch:80, Cost:0.27965
Pass:8, Batch:120, Cost:0.44373
Pass:8, Batch:160, Cost:0.30215
Test:8, Cost:0.44874, ACC:0.80029
Pass:9, Batch:0, Cost:0.60523
Pass:9, Batch:40, Cost:0.47129
Pass:9, Batch:80, Cost:0.22142
Pass:9, Batch:120, Cost:0.39324
Pass:9, Batch:160, Cost:0.26854
Test:9, Cost:0.43634, ACC:0.80823
save models to /home/aistudio/work/emotionclassify.inference.model
['save_infer_model/scale_0']我们先定义三个句子,第一句是中性的,第二句偏向正面,第三句偏向负面。然后把这些句子读取到一个列表中。
1 | # 定义预测数据 |
然后把句子转换成编码,根据数据集的字典,把句子中的单词转换成对应标签。
1 | # 获取结束符号的标签 |
获取输入数据的维度和大小。
1 | # 获取每句话的单词数量 |
将要预测的数据转换成张量,准备开始预测。
1 | # 生成预测数据 |
1 | infer_exe = fluid.Executor(place) #创建推测用的executor |
1 | with fluid.scope_guard(inference_scope):#修改全局/默认作用域(scope), 运行时中的所有变量都将分配给新的scope。 |
'read the book forget the movie'的预测结果为:正面概率为:0.54671,负面概率为:0.45329
'this is a great movie'的预测结果为:正面概率为:0.62144,负面概率为:0.37856
'this is very bad'的预测结果为:正面概率为:0.37344,负面概率为:0.62656预测结果显示这个模型的预测较为准确,输出结果符合人类观察的预期;可以继续调整网络参数、结构,使其能够更好的对文本进行情感分类。
Biggio[22]等人首先针对传统机器学习分类器(如SVM和三层全连接神经网络)的MNIST手写数字识别数据集生成对抗样本。
它通过优化判别函数来误导分类器。
Szegedy[8]等人首次证明了可以通过对图像添加小量的人类察觉不到的扰动误导深度神经网络图像分类器做出错误的分类。他们首先尝试求解让神经网络做出误分类的最小扰动的方程。作者认为,深度神经网络所具有的强大的非线性表达能力和模型的过拟合是可能产生对抗性样本原因之一。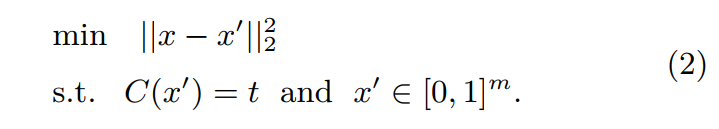
其中,x表示原始图像,x’表示添加微小扰动后的图片,x-x’则表示扰动大小,$\left|x-x^{\prime}\right|_{2}^{2}$表示扰动的L2范数,C()是深度神经网络的分类器。
Szegedy等人引入损失函数,即寻找最小的损失函数添加项,使得神经网络做出误分类,这就将此问题转化成了凸优化过程。
$\min c\left|x-x^{\prime}\right|_{2}^{2}+\mathcal{L}\left(\theta, x^{\prime}, t\right), \quad$ s.t. $\quad x^{\prime} \in[0,1]^{m}$
L( , , )计算分类器的loss
Goodfellow等人[9]认为高维空间下深度神经网络的线性线性行为是导致该问题(存在对抗样本)的根本原因。提出了一种一步生成法来快速生成对抗样本,可以有效计算对抗扰动。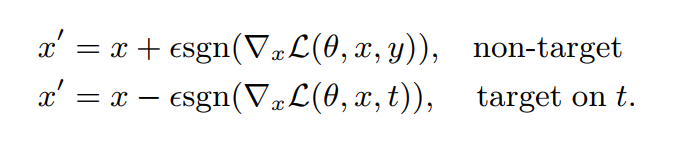
$\eta=\varepsilon \operatorname{sgn}\left(\nabla_{x} \mathcal{L}(\theta, x, t)\right)$
$x$:原始图像
$\eta$:扰动
$\varepsilon$:表示控制扰动大小的自定义参数
$\mathcal{L}$:损失函数
$\operatorname{sgn}$:符号函数
FGSM的核心思想是:通过让扰动方向与梯度方向一致,使损失函数值变化最大,进而使分类器分类结果变化最大。sign函数保证了扰动方向与梯度方向一致;对损失函数求偏导。
FGSM 算法优点是只需一步迭代就能生成对抗样本,并且可以通过控制参数$\varepsilon$生成任意$L_{\infty}$范数距离的对抗样本;缺点是扰动自身抗干扰能力不强,容易受到其他噪声的影响; 另外,模型损失函数与模型输入并不是完全线性的,这说明该算法生成的对抗样本扰动不是最优扰动。
Moosavi-Dezfooli 等人 [32] 通过迭代计算的方法生成能够使分类器模型产生误识别的最小规范对抗扰动,将位于分类边界内的图像逐步推到边界外,直到出现错误分类。作者证明他们生成的扰动比 FGSM 更小,同时有相似的欺骗率。
Deepfool 算法生成对抗样本过程与使用 L-BFGS 生成对抗样本过程类似,主要区别是: Deepfool 算法每次迭代都计算当前样本和各决策边界的距离,然后选择向最近的决策边界迭代生成扰动。
基于雅可比矩阵的显着性图攻击(JSMA)[33]介绍了一种基于计分函数F的雅可比矩阵的方法。 通过迭代操纵对模型输出影响最大的像素,可以将其视为贪婪攻击算法。
对抗攻击文献中通常使用的方法是限制扰动的 L∞或 L2 范数的值以使对抗样本中的扰动无法被人察觉。但 JSMA[33] 提出了限制 L0 范数的方法,即仅改变几个像素的值,而不是扰动整张图像。
针对 FGSM 算法存在的问题, Kurakin 等人[15,31]在 FGSM 算法基础上提出了一种以多步迭代的方式生成对抗样本的方法 BIM。
one-step 方法通过一大步运算增大分类器的损失函数而进行图像扰动,因而可以直接将其扩展为通过多个小步增大损失函数的变体,从而我们得到 Basic Iterative Methods(BIM)
Carlini 和 Wagner[36] 提出了三种对抗攻击方法,通过限制 L∞、L2 和 L0 范数使得扰动无法被察觉。实验证明 defensive distillation (防御性蒸馏)完全无法防御这三种攻击。该算法生成的对抗扰动可以从 unsecured 的网络迁移到 secured 的网络上,从而实现黑盒攻击。
C&W是一种基于目标函数优化的对抗样本攻击算法,其核心思想是:假设对抗样本是一个变量,那么要使其成功攻击分类器模型,必须满足两个条件, 一是其与原始样本的距离要尽可能的小,二是其能够误导分类器模型对其进行错误分类。
Carlini等人[35]试图找到可证明的最强攻击,即找到理论上最小失真的对抗样本的方法。
该攻击基于Reluplex [36],Reluplex是一种用于验证神经网络属性的算法。 它将模型参数F和数据(x,y)编码为线性编程系统的主体,然后求解该系统以检查在x’的邻居中是否存在可以欺骗模型的合格样本x’。 如果我们一直减小搜索区域的半径,直到系统确定不存在一个x’会欺骗模型,那么最后发现的对抗样本被称为标注的真实数据的对抗样本,因为事实证明它与x的相似性最小。
Ground truth攻击是计算分类器精确鲁棒性(最小扰动)的第一项工作。但是,该方法涉及使用可满足性模理论(SMT)求解器,(一种复杂算法, 用于检验一系列理论的可满足性),这将使其效率变慢并且无法扩展到大型网络。近期的研究工作[37,38]提高了 Ground truth攻击的效率。

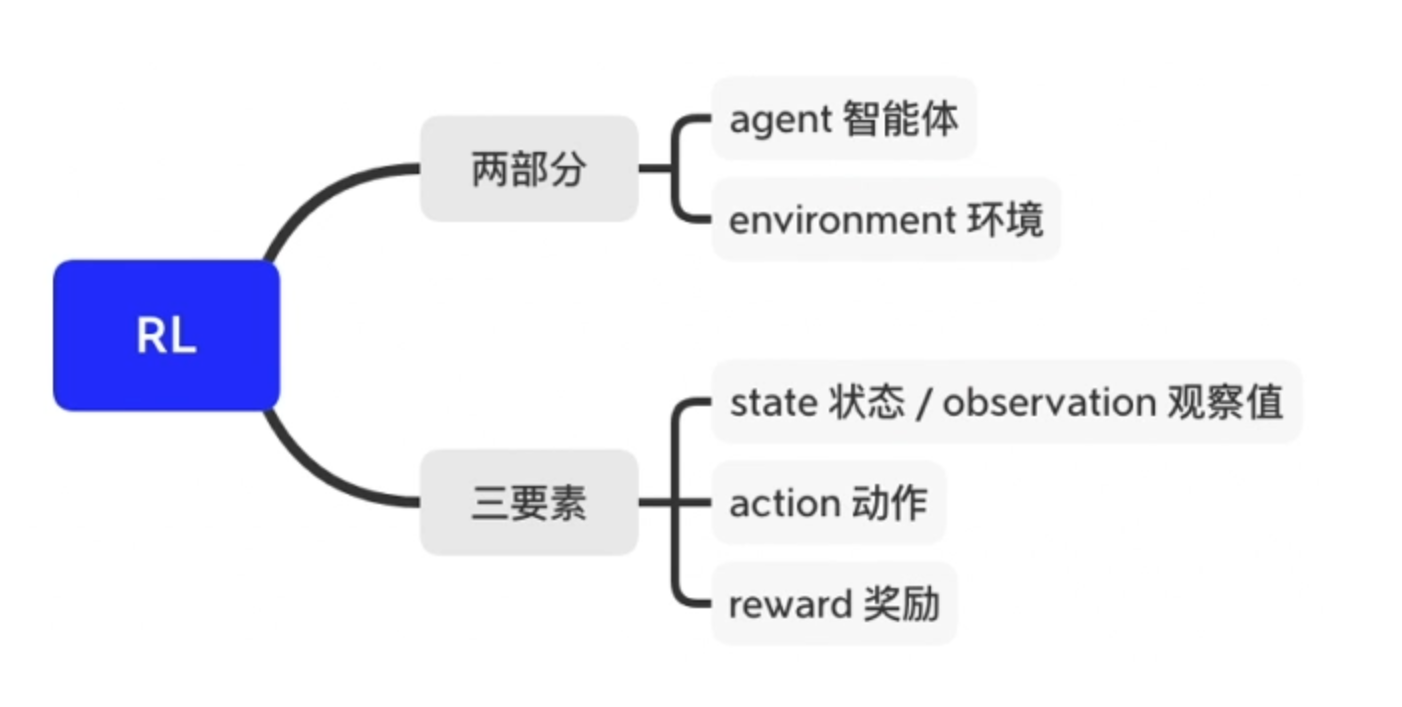
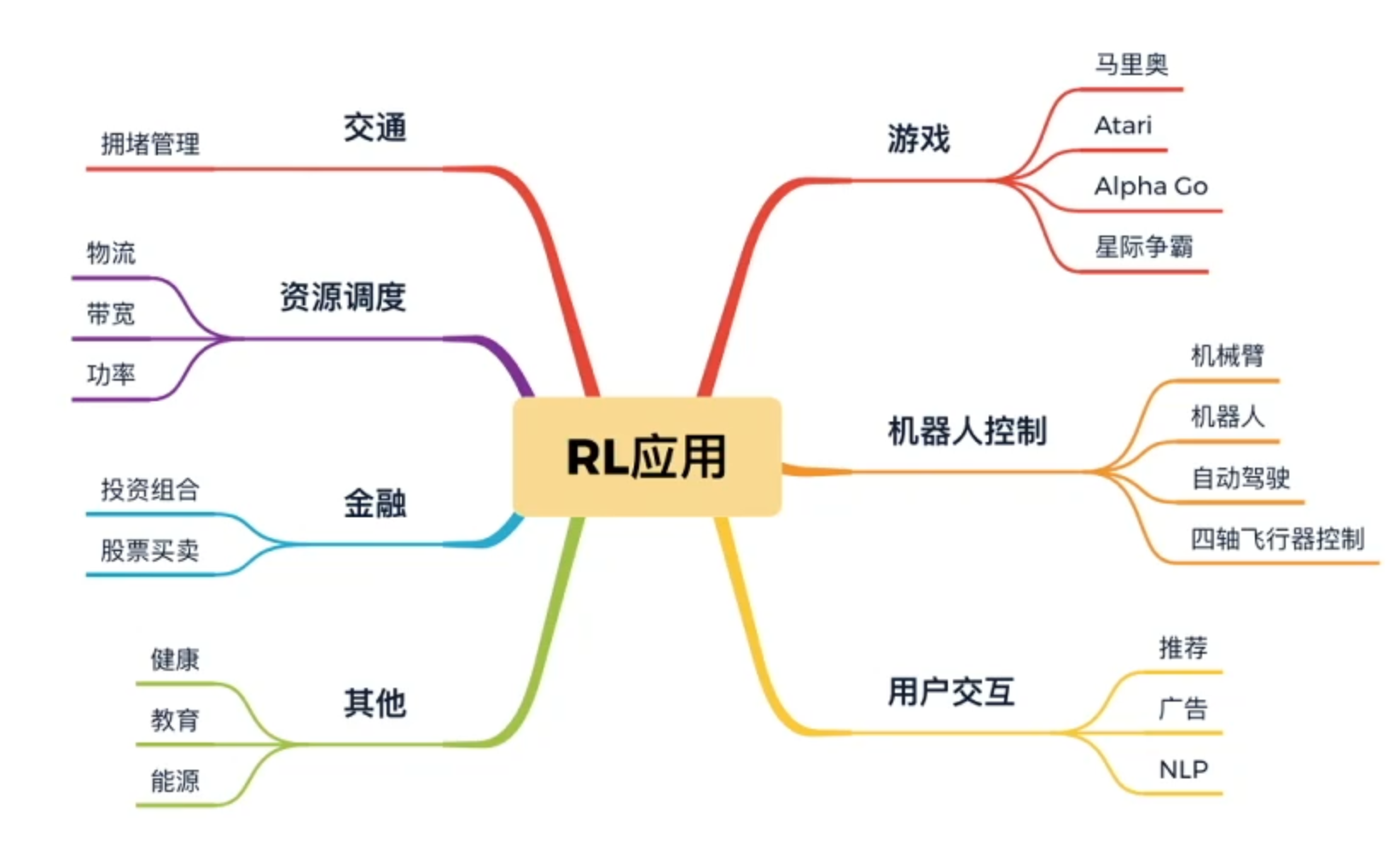
强化学习入门路线:
简单来说就是让机器像人一样学习:
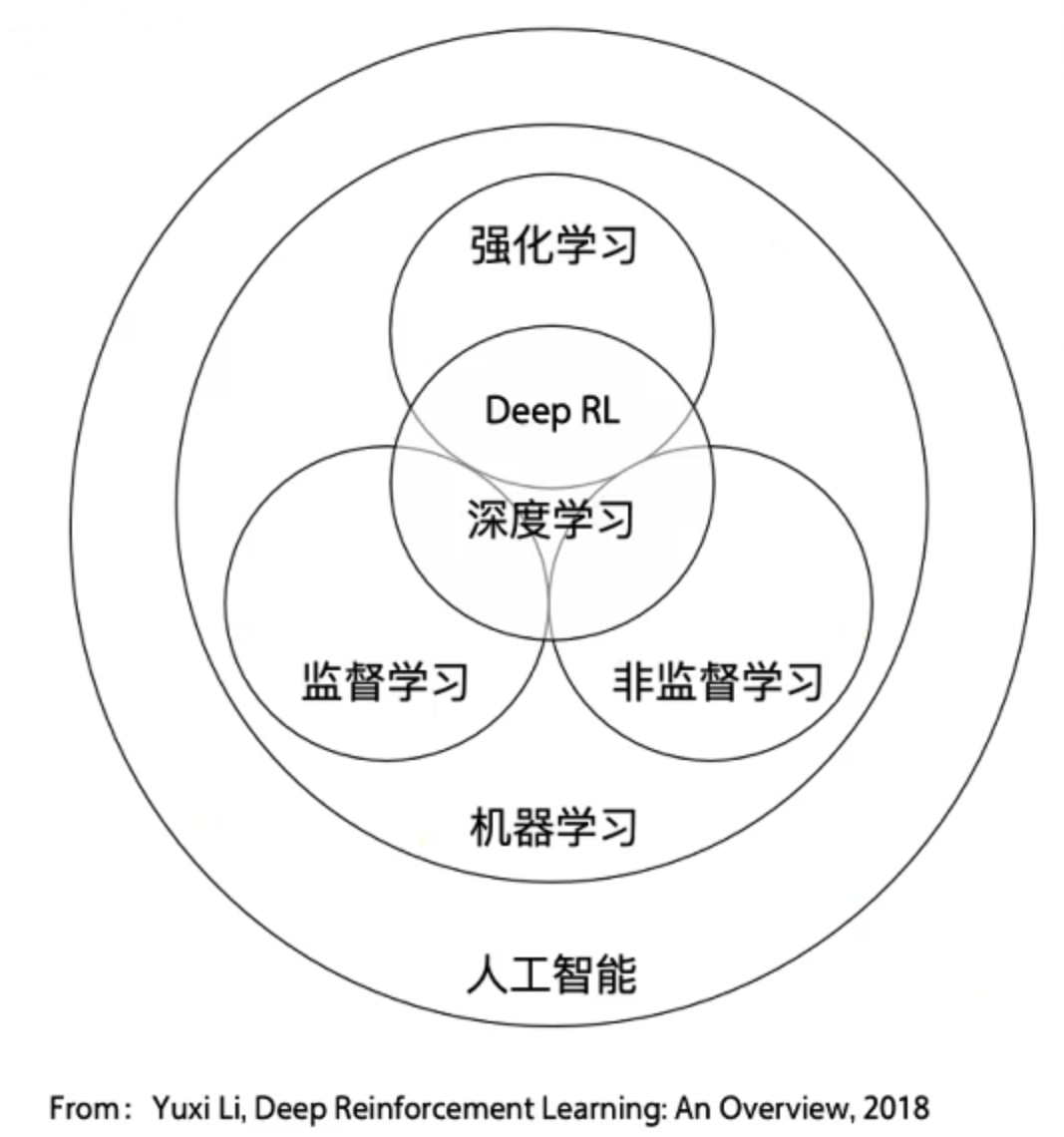
强化学习(英语:Reinforcement learning,简称RL)是机器学习中的一个领域,强调如何基于环境而行动,以取得最大化的预期利益。
核心思想:智能体agent在环境environment中学习,根据环境的状态state(或观测到的observation),执行动作action,并根据环境的反馈reward(奖励)来指导更好的动作。
注意:从环境中获取的状态,有时候叫state,有时候叫observation,这两个其实一个代表全局状态,一个代表局部观测值,在多智能体环境里会有差别,但我们刚开始学习遇到的环境还没有那么复杂,可以先把这两个概念划上等号。
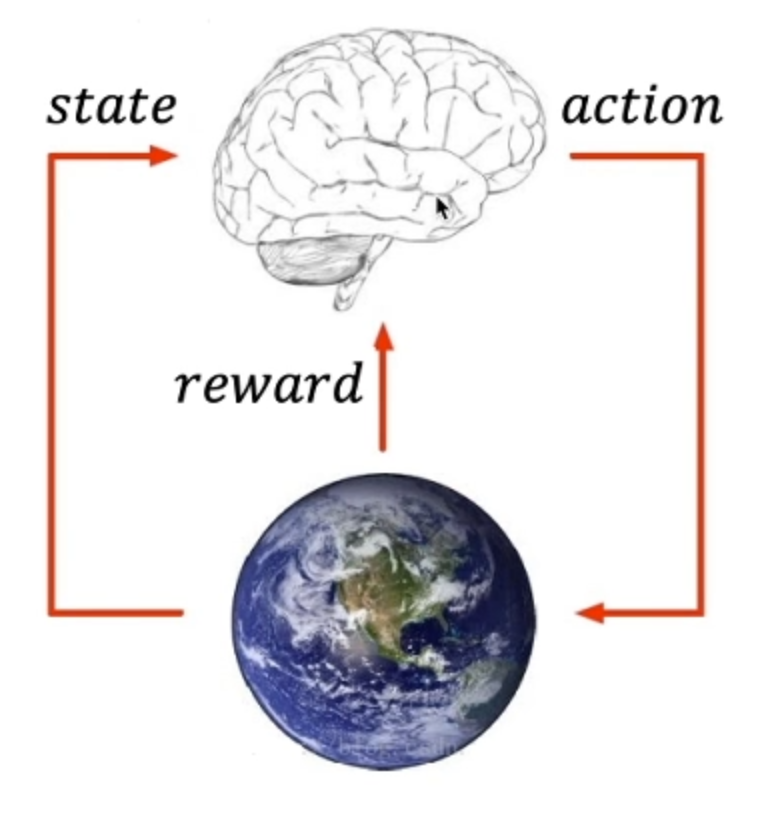
这里地球来表示environment环境,大脑表示agent,agent从environment里面去观察导state状态,然后输出action动作来去和environment做交互,会从环境中得到反馈reward来指导自己的action动作是不是正确的。
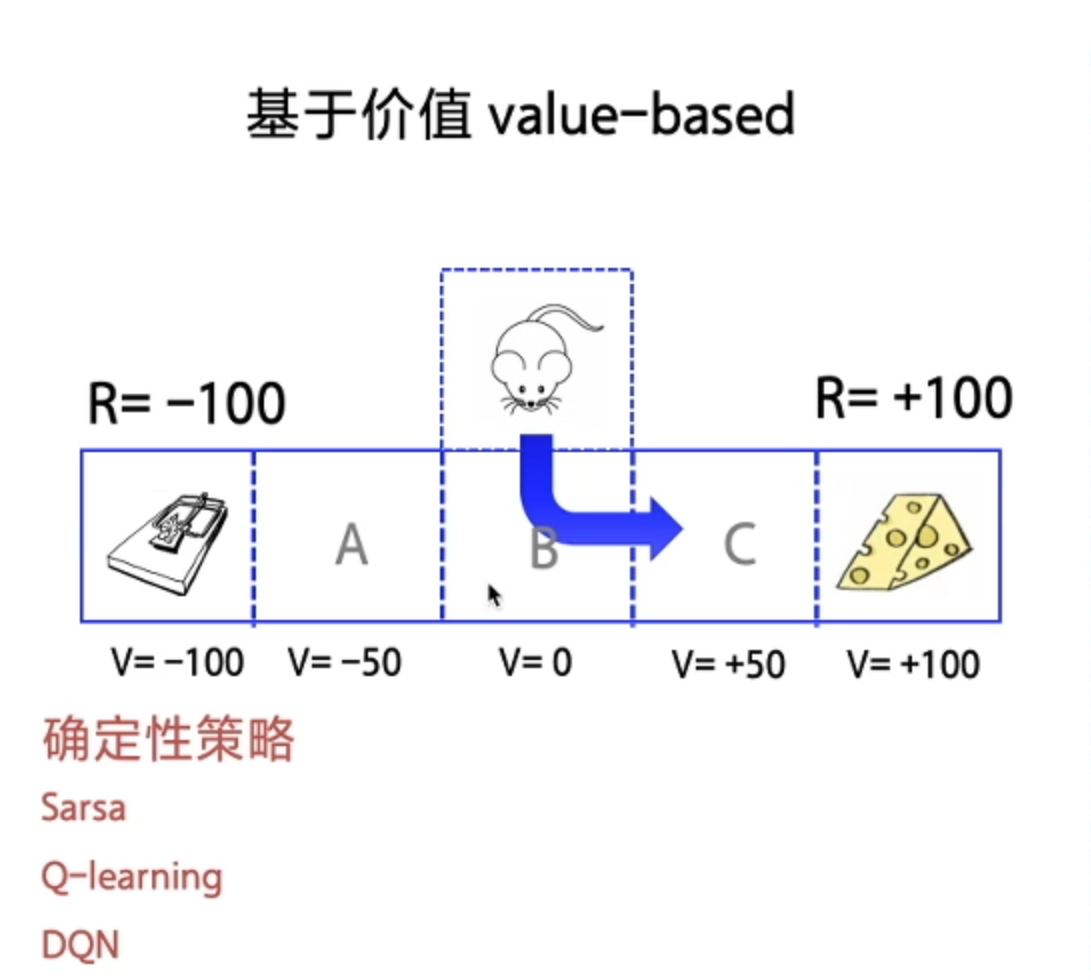
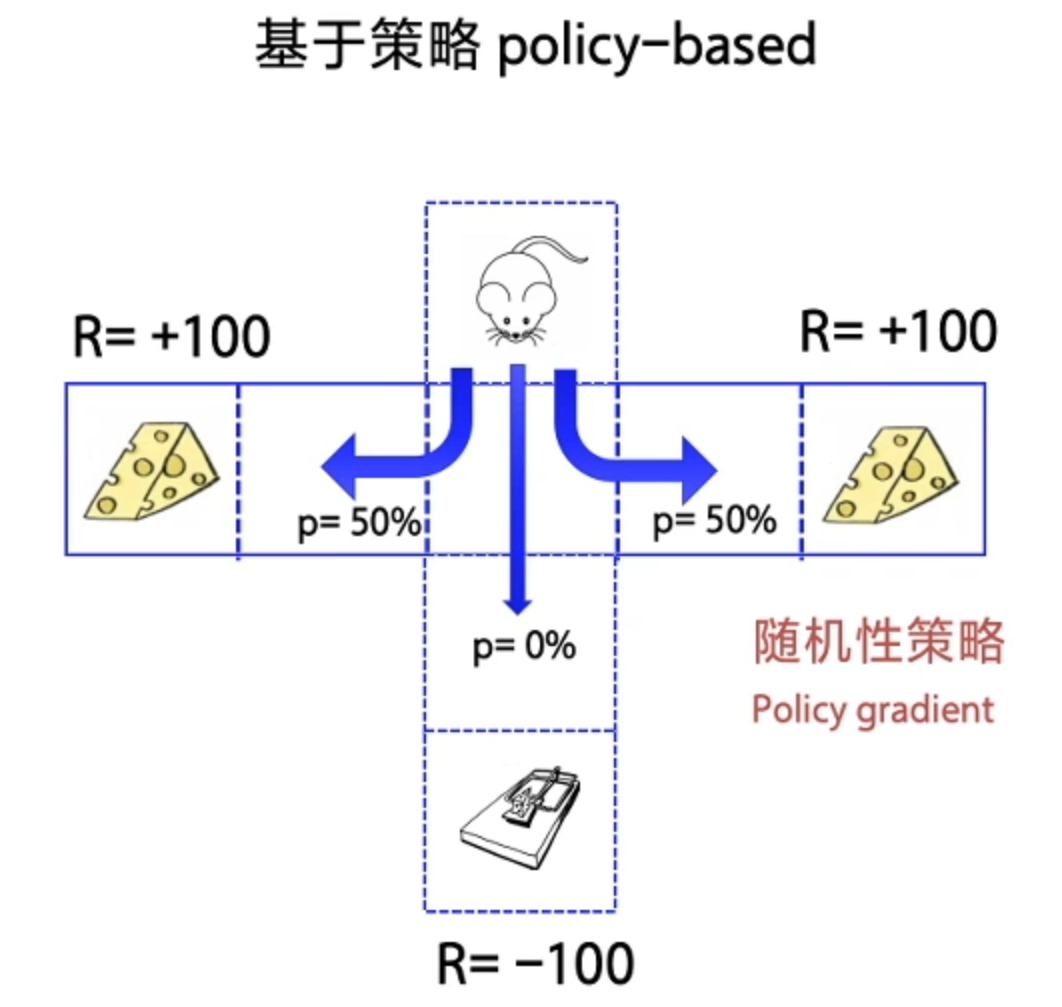
1、基于价值 Value-based (每一步 State 给奖励)—— 最终 Agent 获得每一步最优解(确定性策略)
1 | import parl |
1 | LEARN_FREQ = 5 # 训练频率,不需要每一个step都learn,攒一些新增经验后再learn,提高效率 |
1 | #Model用来定义前向(Forward)网络,用户可以自由的定制自己的网络结构。 |
1 | # from parl.algorithms import DQN # 也可以直接从parl库中导入DQN算法 |
1 | Algorithm定义了具体的算法来更新前向网络(Model),也就是通过定义损失函数来更新Model,和算法相关的计算都放在algorithm中。 |
1 | # replay_memory.py |
1 | # 训练一个episode |
1 | # 创建环境 |