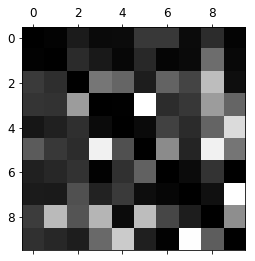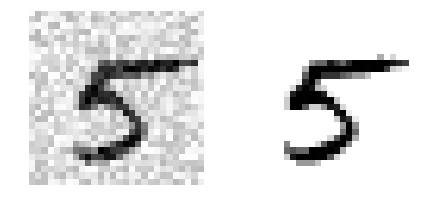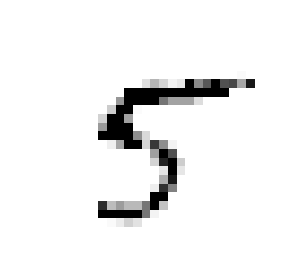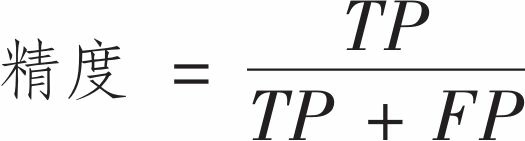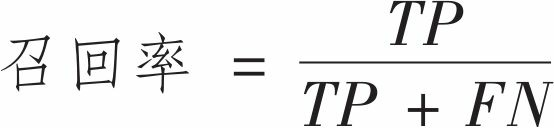Classification分类器|机器学习实战-基于Scikit-Learn和TensorFlow

发表于 更新于 分类于

Classification

监督学习任务（分类）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals

# Common imports
import numpy as np
import os

# to make this notebook's output stable across runs
np.random.seed(42)

# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "classification"

def save_fig(fig_id, tight_layout=True):
    path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
    print("Saving figure", fig_id)
    if tight_layout:
        plt.tight_layout()
    plt.savefig(path, format='png', dpi=300)

MNIST

1
2
3
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784')#获得mnist数据集
mnist
{'data': array([[0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.],
        ...,
        [0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.],
        [0., 0., 0., ..., 0., 0., 0.]]),
 'target': array(['5', '0', '4', ..., '4', '5', '6'], dtype=object),
 'frame': None,
 'categories': {},
1
2
X, y = mnist["data"], mnist["target"]#共70000张图片，每张图片有784个特征，28x28像素，每个特征代表一个像素点的强度
X.shape#查看各个维度的维数
(70000, 784)
1
y.shape
(70000,)
1
28*28
784
1
2
3
4
5
6
7
8
9
10
11
12
13
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
#先来看看数据集中的一个数字， 你只需要随手抓取一个实例的特征向量，将其重新形成一个28×28数组，然后使用Matplotlib的
#imshow（）函数将其显示出来：
some_digit = X[36000]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap = matplotlib.cm.binary,
           interpolation="nearest")
plt.axis("off")

save_fig("some_digit_plot")
plt.show()
Saving figure some_digit_plot

在这里插入图片描述

1
2
3
4
5
def plot_digit(data):
    image = data.reshape(28, 28)
    plt.imshow(image, cmap = matplotlib.cm.binary,
               interpolation="nearest")
    plt.axis("off")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# EXTRA
def plot_digits(instances, images_per_row=10, **options):
    size = 28
    images_per_row = min(len(instances), images_per_row)
    images = [instance.reshape(size,size) for instance in instances]
    n_rows = (len(instances) - 1) // images_per_row + 1
    row_images = []
    n_empty = n_rows * images_per_row - len(instances)
    images.append(np.zeros((size, size * n_empty)))
    for row in range(n_rows):
        rimages = images[row * images_per_row : (row + 1) * images_per_row]
        row_images.append(np.concatenate(rimages, axis=1))
    image = np.concatenate(row_images, axis=0)
    plt.imshow(image, cmap = matplotlib.cm.binary, **options)
    plt.axis("off")
1
2
3
4
5
plt.figure(figsize=(9,9))
example_images = np.r_[X[:12000:600], X[13000:30600:600], X[30600:60000:590]]
plot_digits(example_images, images_per_row=10)
save_fig("more_digits_plot")
plt.show()
Saving figure more_digits_plot

在这里插入图片描述

1
y[36000]
'9'
1
2
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]#创建一个测试集，分成训练集
#（前6万张图像）和测试集（最后1万张图像）
1
2
3
4
import numpy as np
shuffle_index = np.random.permutation(60000)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]
print(X_train.shape)
(60000, 784)

Binary classifier二分类

1
2
3
4
5
#训练一个二元分类器
y_train = y_train.astype(np.int8)#将充满false的数组强制转换为int8
print(y_train_5)
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
[False False  True ... False False False]
1
2
3
4
from sklearn.linear_model import SGDClassifier
#挑选一个分类器并开始训练，SGDClassifier在训练时是完全随机的。
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
SGDClassifier(random_state=42)
1
sgd_clf.predict([some_digit])
array([False])
1
2
3
4
5
#交叉验证是评估模型的好办法
from sklearn.model_selection import cross_val_score
##用cross_val_score（） 函数来评估SGDClassifier模型， 采用K-fold交叉验证法， 3个折叠。
#K-fold交叉验证的意思是将训练集分解成K个折叠（在本例中， 为3折） ， 然后每次留其中1个折叠进行预测， 剩余的折叠用来训练
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
array([0.9334, 0.9644, 0.9568])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone

skfolds = StratifiedKFold(n_splits=3, random_state=42)

for train_index, test_index in skfolds.split(X_train, y_train_5):
    clone_clf = clone(sgd_clf)
    X_train_folds = X_train[train_index]
    y_train_folds = (y_train_5[train_index])
    X_test_fold = X_train[test_index]
    y_test_fold = (y_train_5[test_index])

    clone_clf.fit(X_train_folds, y_train_folds)
    y_pred = clone_clf.predict(X_test_fold)
    n_correct = sum(y_pred == y_test_fold)
    print(n_correct / len(y_pred))
D:\Anaconda3\envs\learn\lib\site-packages\sklearn\model_selection\_split.py:297: FutureWarning: Setting a random_state has no effect since shuffle is False. This will raise an error in 0.24. You should leave random_state to its default (None), or set shuffle=True.
  FutureWarning
0.9334
0.9644
0.9568
1
2
3
4
5
6
from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
    def fit(self, X, y=None):
        pass
    def predict(self, X):
        return np.zeros((len(X), 1), dtype=bool)
1
2
3
4
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")
#准确率超过90%，这是因为只有大约10%的图像是数字9，所以如果你猜一张图不是9， 90%的时间你都是正确的
#说明准确率通常无法成为分类器的首要性能指标
array([0.90855, 0.9093 , 0.9111 ])
1
2
3
from sklearn.model_selection import cross_val_predict

y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
1
2
3
from sklearn.metrics import confusion_matrix

confusion_matrix(y_train_5, y_train_pred)
array([[53124,  1455],
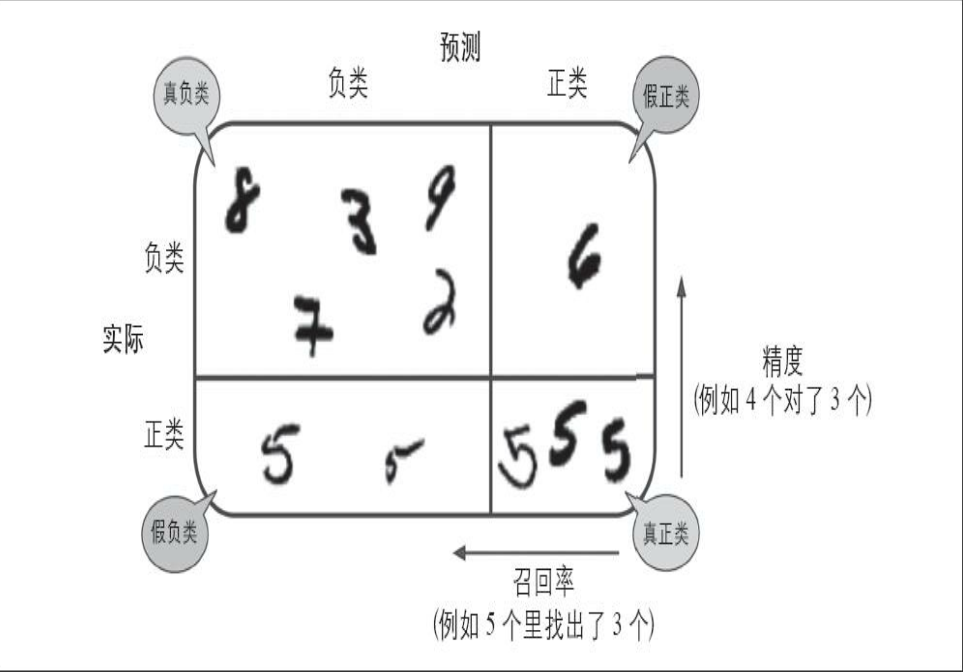
       [ 949,  4472]], dtype=int64)
1
2
3
4
5
6
7
8
y_train_perfect_predictions = y_train_5
'''混淆矩阵中的行表示实际类别， 列表示预测类别。 本例中第一行
表示所有“非5”（负类） 的图片中： 53065张被正确地分为“非5”类别
（真负类） ， 1455张被错误地分类成了“5”（假正类） ； 第二行表示
所有“5”（正类） 的图片中： 949张被错误地分为“非5”类别（假负
类） ， 4472张被正确地分在了“5”这一类别（真正类） 。 一个完美的
分类器只有真正类和真负类， 所以它的混淆矩阵只会在其对角线（左
上到右下） 上有非零值：'''
1
confusion_matrix(y_train_5, y_train_perfect_predictions)
array([[54579,     0],
       [    0,  5421]], dtype=int64)

正类预测的准确度也可称为分类器的精度

在这里插入图片描述
TP是真正类的数量， FP是假正类的数量。

精度通常与另一个指标一起使用，这个指标就是召回率（recall），也称为灵敏度（sensitivity）或者真正类率（TPR）：它是分类器正确检测到的正类实例的比率
在这里插入图片描述

FN是假负类的数量。

图解混淆矩阵在这里插入图片描述

精度和召回率
1
2
3
4
5
from sklearn.metrics import precision_score, recall_score

precision_score(y_train_5, y_train_pred)#TP/(TP+FP)    4472/ (4472+ 1455)
#array([[53124,  1455],     TN   FP
 #          [ 949,  4472]]   FN    TP
0.754513244474439
1
recall_score(y_train_5, y_train_pred)#TP/(TP+FN)  4472/(4472+949)
0.8249400479616307

因此我们可以很方便地将精度和召回率组合成一个单一的指标，称为F1分数。 当你需要一个简单的方法来比较两种分类器时， 这是个非常不错的指标。 F1分数是精度和召回率的谐波平均值 。 正常的平均值平等对待所有的值， 而谐波平均值会给予较低的值更高的权重。 因此， 只有当召回率和精度都很高时， 分类器才能得到较高的F1分数

F1分数
在这里插入图片描述

1
2
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)#4472/ (4472+ (949+ 1455)/2)
0.7881565033486078
1
4472/ (4472+ (949+ 1455)/2)
0.7881565033486078

精度/召回率权衡

Scikit-Learn不允许直接设置阈值，但是可以访问它用于预测的决策分数。不是调用分类器的predict（）方法，而是调用decision_function（）方法，这个方法返回每个实例的分数，然后就可以根据这些分数，使用任意阈值进行预测了：

1
2
y_scores = sgd_clf.decision_function([some_digit])
y_scores
array([ 161855.74572176])
1
2
threshold = 0
y_some_digit_pred = (y_scores > threshold)
1
y_some_digit_pred

array([ True], dtype=bool)
SGDClassifier分类器使用的阈值是0， 所以前面的代码返回结果
与predict（） 方法一样（也就是True） 。 我们来试试提升阈值：

1
2
3
threshold = 200000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
array([False], dtype=bool)

这证明了提高阈值确实可以降低召回率。 这张图确实是5， 当阈值为0时， 分类器可以检测到该图， 但是当阈值提高到200000时， 就错过了这张图。

  • 那么要如何决定使用什么阈值呢？ 首先， 使用cross_val_predict（） 函数获取训练集中所有实例的分数， 但是这次需要它返回的是决策分数而不是预测结果：
    1
    2
    y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
                                 method="decision_function")

Note: there is an issue introduced in Scikit-Learn 0.19.0 where the result of cross_val_predict() is incorrect in the binary classification case when using method="decision_function", as in the code above. The resulting array has an extra first dimension full of 0s. We need to add this small hack for now to work around this issue:

1
y_scores.shape
(60000, 2)
1
2
3
# hack to work around issue #9589 introduced in Scikit-Learn 0.19.0
if y_scores.ndim == 2:
    y_scores = y_scores[:, 1]

有了这些分数， 可以使用precision_recall_curve（） 函数来计算
所有可能的阈值的精度和召回率：

1
2
3
from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

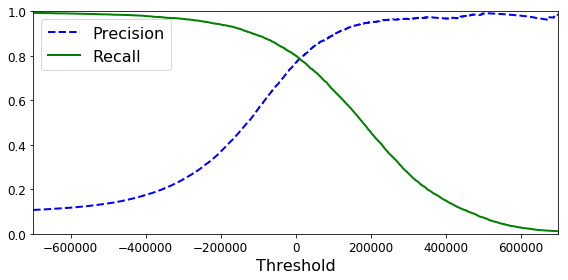
最后， 使用Matplotlib绘制精度和召回率相对于阈值的函数图

1
2
3
4
5
6
7
8
9
10
11
12
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
    plt.xlabel("Threshold", fontsize=16)
    plt.legend(loc="upper left", fontsize=16)
    plt.ylim([0, 1])

plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
save_fig("precision_recall_vs_threshold_plot")
plt.show()
Saving figure precision_recall_vs_threshold_plot

在这里插入图片描述

1
(y_train_pred == (y_scores > 0)).all()
True
1
y_train_pred_90 = (y_scores > 70000)
1
precision_score(y_train_5, y_train_pred_90)
0.86592051164915484
1
recall_score(y_train_5, y_train_pred_90)
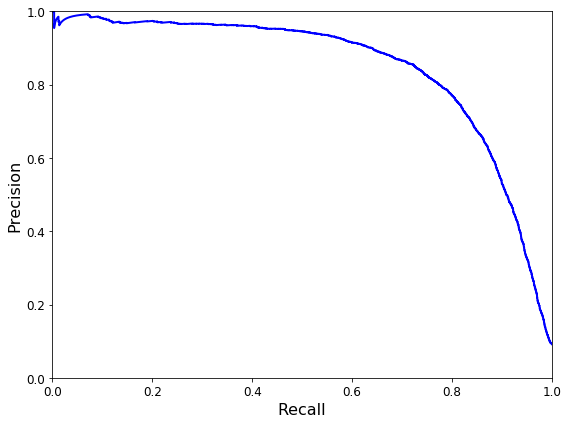
0.69931746910164172
1
2
3
4
5
6
7
8
9
10
def plot_precision_vs_recall(precisions, recalls):
    plt.plot(recalls, precisions, "b-", linewidth=2)
    plt.xlabel("Recall", fontsize=16)
    plt.ylabel("Precision", fontsize=16)
    plt.axis([0, 1, 0, 1])

plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
save_fig("precision_vs_recall_plot")
plt.show()
Saving figure precision_vs_recall_plot

在这里插入图片描述

ROC 曲线

ROC叫受试者工作特征曲线。它与精度/召回率曲线非常相似，但绘制的不
是精度和召回率，而是真正类率（召回率的另一名称）和假正类率（FPR）。 FPR是被错误分为正类的负类实例比率。它等于1减去真负类率（TNR），后者是被正确分类为负类的负类实例比率，也称为特异度。因此， ROC曲线绘制的是灵敏度和（1-特异度）的关系。

要绘制ROC曲线，首先需要使用roc_curve（）函数计算多种阈值的TPR和FPR：
1
2
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
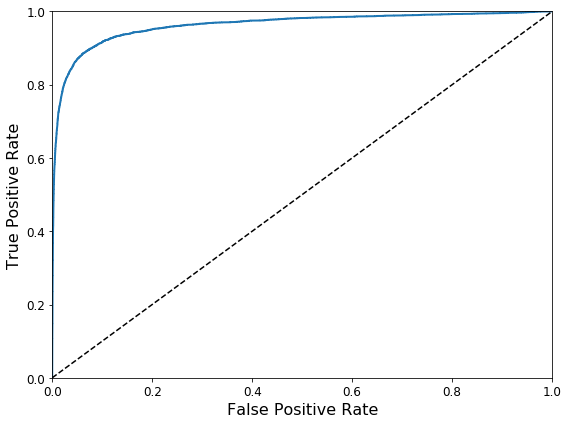
然后，使用Matplotlib绘制FPR对TPR的曲线。
1
2
3
4
5
6
7
8
9
10
11
def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--')
    plt.axis([0, 1, 0, 1])
    plt.xlabel('False Positive Rate', fontsize=16)
    plt.ylabel('True Positive Rate', fontsize=16)

plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
save_fig("roc_curve_plot")
plt.show()
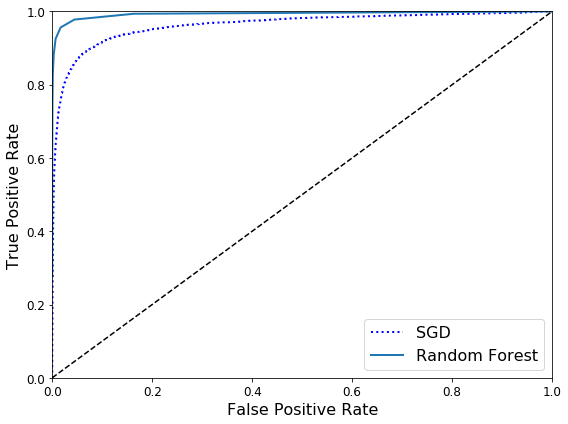
Saving figure roc_curve_plot

在这里插入图片描述
召回率（TPR） 越高， 分类器产生的假正类（FPR） 就越多。 虚线表示纯随机分类器的ROC曲线；一个优秀的分类器应该离这条线越远越好（向左上角） 。

　　有一种比较分类器的方法是测量曲线下面积（AUC） 。 完美的分类器的ROC AUC等于1， 而纯随机分类器的ROC AUC等于0.5。Scikit-Learn提供计算ROC AUC的函数：

1
2
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
0.96244965559671547

由于ROC曲线与精度/召回率（或PR） 曲线非常相似，有时候我们会选择使用哪种曲线，有一个经验法则是， 当正类非常少见或者你更关注假正类而不是假负类时， 你应该选择PR曲线， 反之则是ROC曲线。PR曲线可以暗示分类器还有改进的空间（曲线更接近右上角）。

下面训练一个RandomForestClassifier分类器，并比较它和SGDClassifier分类器的ROC曲线和ROC AUC分数。 

1
2
3
4
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
                                    method="predict_proba")
1
2
y_scores_forest = y_probas_forest[:, 1] # score = proba of positive class
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)
1
2
3
4
5
6
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.legend(loc="lower right", fontsize=16)
save_fig("roc_curve_comparison_plot")
plt.show()
Saving figure roc_curve_comparison_plot

在这里插入图片描述
如上图所示， RandomForestClassifier的ROC曲线看起来比SGDClassifier好很多： 它离左上角更接近。 因此它的ROC AUC分数也高得多：

1
roc_auc_score(y_train_5, y_scores_forest)
0.99312433660038291
1
2
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3)
precision_score(y_train_5, y_train_pred_forest)#精度
0.98529734474434938
1
recall_score(y_train_5, y_train_pred_forest)#召回率
0.82826046854823832
再测一测精度和召回率的分数： 98.5%的精度和82.8%的召回率， 也还不错！

Multiclass classification多类别分类器

二元分类器在两个类别中区分，而多类别分类器（也称为多项分类器）可以区分两个以上的类别。

Scikit-Learn可以检测到你尝试使用二元分类算法进行多类别分类任务，它会自动运行OvA（SVM分类器除外，它会使用OvO）。我们用SGDClassifier试试：

1
2
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
array([ 5.])

可以调用decision_function（ ） 方法，Scikit-Learns实际上训练了10个二元分类器，获得它们对图片的决策分数， 然后选择了分数最高的类别。

1
2
some_digit_scores = sgd_clf.decision_function([some_digit])
some_digit_scores
array([[-311402.62954431, -363517.28355739, -446449.5306454 ,
        -183226.61023518, -414337.15339485,  161855.74572176,
        -452576.39616343, -471957.14962573, -518542.33997148,
        -536774.63961222]])
1
np.argmax(some_digit_scores)#最好分是对应数字5这个类别
5
1
sgd_clf.classes_
array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9.])
1
sgd_clf.classes_[5]#当训练分类器时， 目标类别的列表会存储在classes_这个属性中， 按值的大小排序。
5.0
1
2
3
4
from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(X_train, y_train)
ovo_clf.predict([some_digit])
array([ 5.])
1
len(ovo_clf.estimators_)
45
1
2
forest_clf.fit(X_train, y_train)
forest_clf.predict([some_digit])
array([ 5.])
1
forest_clf.predict_proba([some_digit])
array([[ 0.1,  0. ,  0. ,  0.1,  0. ,  0.8,  0. ,  0. ,  0. ,  0. ]])
1
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
array([ 0.84063187,  0.84899245,  0.86652998])
1
2
3
4
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")
array([ 0.91011798,  0.90874544,  0.906636  ])

错误分析

一般机器学习项目包含：探索数据准备的选项， 尝试多个模型， 列出最佳模型并用GridSearchCV对其超参数进行微调， 尽可能自动化。假设当前已经找到了一个由潜力的模型，现在想进一步微调参数。
首先， 看看混淆矩阵。 就像之前做的， 使用cross_val_predict（）函数进行预测， 然后调用confusion_matrix（） 函数：

1
2
3
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx
array([[5725,    3,   24,    9,   10,   49,   50,   10,   39,    4],
       [   2, 6493,   43,   25,    7,   40,    5,   10,  109,    8],
       [  51,   41, 5321,  104,   89,   26,   87,   60,  166,   13],
       [  47,   46,  141, 5342,    1,  231,   40,   50,  141,   92],
       [  19,   29,   41,   10, 5366,    9,   56,   37,   86,  189],
       [  73,   45,   36,  193,   64, 4582,  111,   30,  193,   94],
       [  29,   34,   44,    2,   42,   85, 5627,   10,   45,    0],
       [  25,   24,   74,   32,   54,   12,    6, 5787,   15,  236],
       [  52,  161,   73,  156,   10,  163,   61,   25, 5027,  123],
       [  43,   35,   26,   92,  178,   28,    2,  223,   82, 5240]])
1
2
3
4
5
6
def plot_confusion_matrix(matrix):
    """If you prefer color and a colorbar"""
    fig = plt.figure(figsize=(8,8))
    ax = fig.add_subplot(111)
    cax = ax.matshow(matrix)
    fig.colorbar(cax)
1
2
3
plt.matshow(conf_mx, cmap=plt.cm.gray)
save_fig("confusion_matrix_plot", tight_layout=False)
plt.show()
Saving figure confusion_matrix_plot

在这里插入图片描述
混淆矩阵看起来很不错，因为大多数图片都在主对角线上，这说明它们被正确分类。

让我们把焦点放在错误上。首先，你需要将混淆矩阵中的每个值除以相应类别中的图片数量，这样你比较的就是错误率而不是错误的绝对值（后者对图片数量较多的类别不公平）：

1
2
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums

用0填充对角线，只保留错误，重新绘制结果：

1
2
3
4
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
save_fig("confusion_matrix_errors_plot", tight_layout=False)
plt.show()
Saving figure confusion_matrix_errors_plot

在这里插入图片描述
　　现在可以清晰地看到分类器产生的错误种类了。 记住， 每行代表实际类别， 而每列表示预测类别。 第8列和第9列整体看起来非常亮，说明有许多图片被错误地分类为数字8或数字9了。 同样， 类别8和类别9的行看起来也偏亮， 说明数字8和数字9经常会跟其他数字混淆。相反， 一些行很暗， 比如行1， 这意味着大多数数字1都被正确地分类（有一些与数字8弄混， 但仅此而已） 。 注意， 错误不是完全对称的， 比如， 数字5被错误分类为数字8的数量比数字8被错误分类为数字5的数量要更多。
　　分析混淆矩阵通常可以帮助你深入了解如何改进分类器。 通过上面那张图来看， 你的精力可以花在改进数字8和数字9的分类， 以及修正数字3和数字5的混淆上。

分析单个的错误也可以为分类器提供洞察： 它在做什么？ 它为什
么失败？ 但这通常更加困难和耗时。 例如， 我们来看看数字3和数字5
的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]

plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
save_fig("error_analysis_digits_plot")
plt.show()
Saving figure error_analysis_digits_plot

在这里插入图片描述
　　左侧的两个5×5矩阵显示了被分类为数字3的图片，右侧的两个5×5矩阵显示了被分类为数字5的图片。分类器弄错的数字（即左下方和右上方的矩阵）里，确实有一些写得非常糟糕，即便是人类也很难做出区分（例如，第8行第1列的数字5看起来真的很像数字3）。然而，对我们来说，大多数错误分类的图片看起来还是非常明显的错误，我们很难理解分类器为什么会弄错。 原因在于，我们使用的简单的SGDClassifier模型是一个线性模型。它所做的就是为每个像素分配一个各个类别的权重，当它看到新的图像时，将加权后的像素强度汇总，从而得到一个分数进行分类。而数字3和数字5只在一部分像素位上有区别，所以分类器很容易将其弄混。
数字3和数字5之间的主要区别是在于连接顶线和下方弧线的中间那段小线条的位置。如果你写的数字3将连接点略往左移，分类器就可能将其分类为数字5，反之亦然。换言之，这个分类器对图像移位和旋转非常敏感。因此，减少数字3和数字5混淆的方法之一，就是对图片进行预处理， 确保它们位于中心位置并且没有旋转。 这也同样有助于减少其他错误。

Multilabel classification多标签分类

　　    到目前为止，每个实例都只会被分在一个类别里。而在某些情况下，你希望分类器为每个实例产出多个类别。例如，人脸识别的分类器：如果在一张照片里识别出多个人怎么办？当然，应该为识别出来的每个人都附上一个标签。假设分类器经过训练，已经可以识别出三张脸——爱丽丝、鲍勃和查理，那么当看到一张爱丽丝和查理的照片时，它应该输出[1， 0， 1]（意思是“是爱丽丝，不是鲍勃，是查理”）这种输出多个二元标签的分类系统称为多标签分类系统。
来看一个例子：

1
2
3
4
5
6
7
8
from sklearn.neighbors import KNeighborsClassifier

y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)

这段代码会创建一个y_multilabel数组，其中包含两个数字图片的目标标签：第一个表示数字是否是大数（7、 8、 9），第二个表示是否为奇数。下一行创建一个KNeighborsClassifier实例（它支持多标签分类，不是所有的分类器都支持），然后使用多个目标数组对它进行训练。现在用它做一个预测，注意它输出的两个标签：

KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=5, p=2,
           weights='uniform')
1
knn_clf.predict([some_digit])
array([[False,  True]], dtype=bool)

结果是正确的！数字5确实不大（False），为奇数（True）。
评估多标签分类器的方法很多，如何选择正确的度量指标取决于你的项目。比如方法之一是测量每个标签的F1分数（或者是之前讨论过的任何其他二元分类器指标），然后简单地平均。下面这段代码计算所有标签的平均F1分数：

1
2
y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)
f1_score(y_multilabel, y_train_knn_pred, average="macro")
0.97709078477525002

这里假设了所有的标签都同等重要， 但实际可能不是这样。 特别是， 如果训练的照片里爱丽丝比鲍勃和查理要多很多， 你可能想给区分爱丽丝的分类器更高的权重。 一个简单的办法是给每个标签设置一个等于其自身支持的权重（也就是具有该目标标签的实例的数量） 。只需要在上面的代码中设置average=”weighted”即可。

Multioutput classification多输出-多类别分类

举个例子：为了说明这一点，构建一个系统去除图片中的噪声。给它输入一张有噪声的图片，它将（希望）输出一张干净的数字图片，跟其他MNIST图片一样，以像素强度的一个数组作为呈现方式。请注意，这个分类器的输出是多个标签（一个像素点一个标签），每个标签可以有多个值（像素强度范围为0到225）。所以这是个多输出分类器系统的例子

还先从创建训练集和测试集开始，使用NumPy的randint（）函数为MNIST图片的像素强度增加噪声。目标是将图片还原为原始图片：

1
2
3
4
5
6
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
1
2
3
4
5
some_index = 5500
plt.subplot(121); plot_digit(X_test_mod[some_index])
plt.subplot(122); plot_digit(y_test_mod[some_index])
save_fig("noisy_digit_example_plot")
plt.show()
Saving figure noisy_digit_example_plot

在这里插入图片描述
左边是有噪声的输入图片， 右边是干净的目标图片。 现在通过训练分类器， 清洗这张图片：

1
2
3
4
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)
save_fig("cleaned_digit_example_plot")
Saving figure cleaned_digit_example_plot

在这里插入图片描述

看起来这张图片离目标足够接近了。
`阅读《机器学习实战-基于Scikit-Learn和TensorFlow》这本书第三章，上述笔记基本参考此书。