常用的向量与矩阵的范数总结[L0、L1、L2范数]

发表于 更新于 分类于

向量的范数

首先定义一个向量为：x=[-5，6，8, -10]
1-范数：

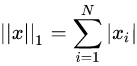在这里插入图片描述，即向量的各个元素的绝对值之和，matlab调用函数norm(x, 1) 。则上述x的1-范数结果是29

2-范数：

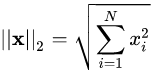在这里插入图片描述，Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，matlab调用函数norm(x, 2)。

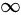在这里插入图片描述-范数：

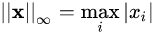在这里插入图片描述，即所有向量元素绝对值中的最大值，matlab调用函数norm(x, inf)。

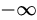在这里插入图片描述-范数：

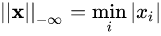在这里插入图片描述，即所有向量元素绝对值中的最小值，matlab调用函数norm(x, -inf)。

p-范数：

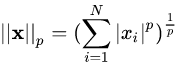在这里插入图片描述，即向量元素绝对值的p次方和的1/p次幂，matlab调用函数norm(x, p)。

矩阵范数

矩阵的1范数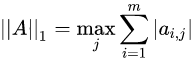
在这里插入图片描述列和范数，即所有矩阵列向量绝对值之和的最大值，矩阵的每一列上的元素绝对值先求和，再从中取个最大的（列和最大）。matlab调用函数norm(A, 1)。

矩阵的2范数：
矩阵的2范数即：矩阵$A^{T} A$的最大特征值开平方根。

矩阵的无穷范数：
矩阵的每一行上的元素绝对值先求和，再从中取个最大的（行和最大）

L0范数和L1范数

L0范数是指向量中非零元素的个数。如果用L0规则化一个参数矩阵W，就是希望W中大部分元素是零，实现稀疏。

L1范数是指向量中各个元素的绝对值之和，也叫”系数规则算子（Lasso regularization）“。L1范数也可以实现稀疏，通过将无用特征对应的参数W置为零实现。

L0和L1都可以实现稀疏化，不过一般选用L1而不用L0，原因包括：1）L0范数很难优化求解（NP难）；2）L1是L0的最优凸近似，比L0更容易优化求解。（这一段解释过于数学化，姑且当做结论记住）
稀疏化的好处是是什么？
1）特征选择
​实现特征的自动选择，去除无用特征。稀疏化可以去掉这些无用特征，将特征对应的权重置为零。
2）可解释性（interpretability）​
例如判断某种病的患病率时，最初有1000个特征，建模后参数经过稀疏化，最终只有5个特征的参数是非零的，那么就可以说影响患病率的主要就是这5个特征。

L2范数

L2范数​​是指向量各元素的平方和然后开方，用在回归模型中也称为岭回归（Ridge regression）。
L2避免过拟合的原理是：让L2范数的规则项||W||2 尽可能小，可以使得W每个元素都很小，接近于零，但是与L1不同的是，不会等于0；这样得到的模型抗干扰能力强，参数很小时，即使样本数据x发生很大的变化，模型预测值y的变化也会很有限。

参考链接：https://www.cnblogs.com/MengYan-LongYou/p/4050862.html

　　　　 https://blog.csdn.net/Michael__Corleone/article/details/75213123