端到端的机器学习项目，预测房价

发表于 更新于 分类于

端到端的机器学习项目

主要步骤：
1.观察大局。
2.获得数据。
3.从数据探索和可视化中获得洞见。
4.机器学习算法的数据准备。
5.选择和训练模型。
6.微调模型。
7.展示解决方案。
8.启动、监控和维护系统。

使用的数据集

选用StatLib库中选择了加州住房价格的数据集，该数据集基于1990年加州人口普查的数据。
链接：https://pan.baidu.com/s/10N6CHN9yxMvG1HHPL6yX2g
提取码：xpzs

观察大局

首先要做的事是使用加州人口普查的数据建立起加州的房价模型。 数据中有许多指标， 诸如每个街区的人口数量、 收入中位数、 房价中位数等。 街区是美国人口普查局发布样本数据的最小地理单位（一个街区通常人口数为600～3000人） 。 这里， 我们将其简称为“区域”。

获得数据

所有数据——一个以逗号来分割之的CSV文档housing.csv
首先使用pandas来加载数据

1
2
3
4
5
import pandas as pd
HOUSING_PATH = os.path.join("datasets", "housing")
def load_housing_data(housing_path=HOUSING_PATH):
    csv_path = os.path.join(housing_path, "housing.csv")
    return pd.read_csv(csv_path)

此函数会返回一个包含所有数据的Pandas DataFrame对象。
用DataFrame的head()方法查看数据集的前五行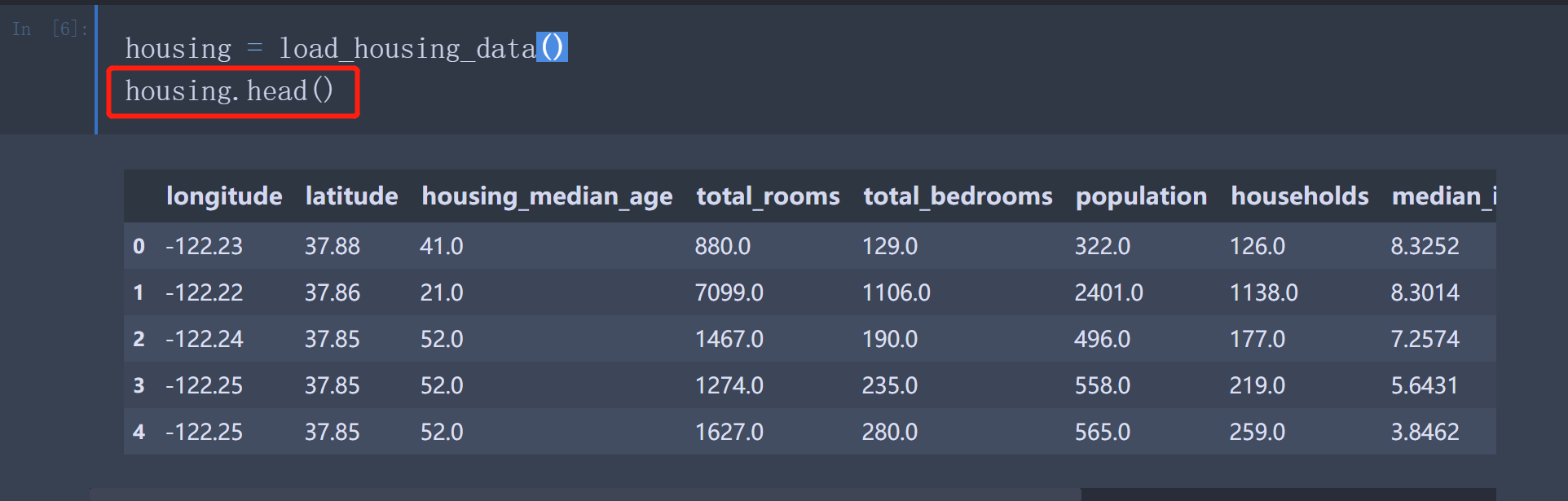
在这里插入图片描述
每一行代表一个区， 总共有10个属性（上图中可以看到8个）longitude， latitude， housing_median_age， total_rooms，total_bed rooms， population， households， median_income，median_house_value以及ocean_proximity。
之后通过info()方法可以快速获取数据集的简单描述，比如总函数，每个属性的类型和非空值的数量。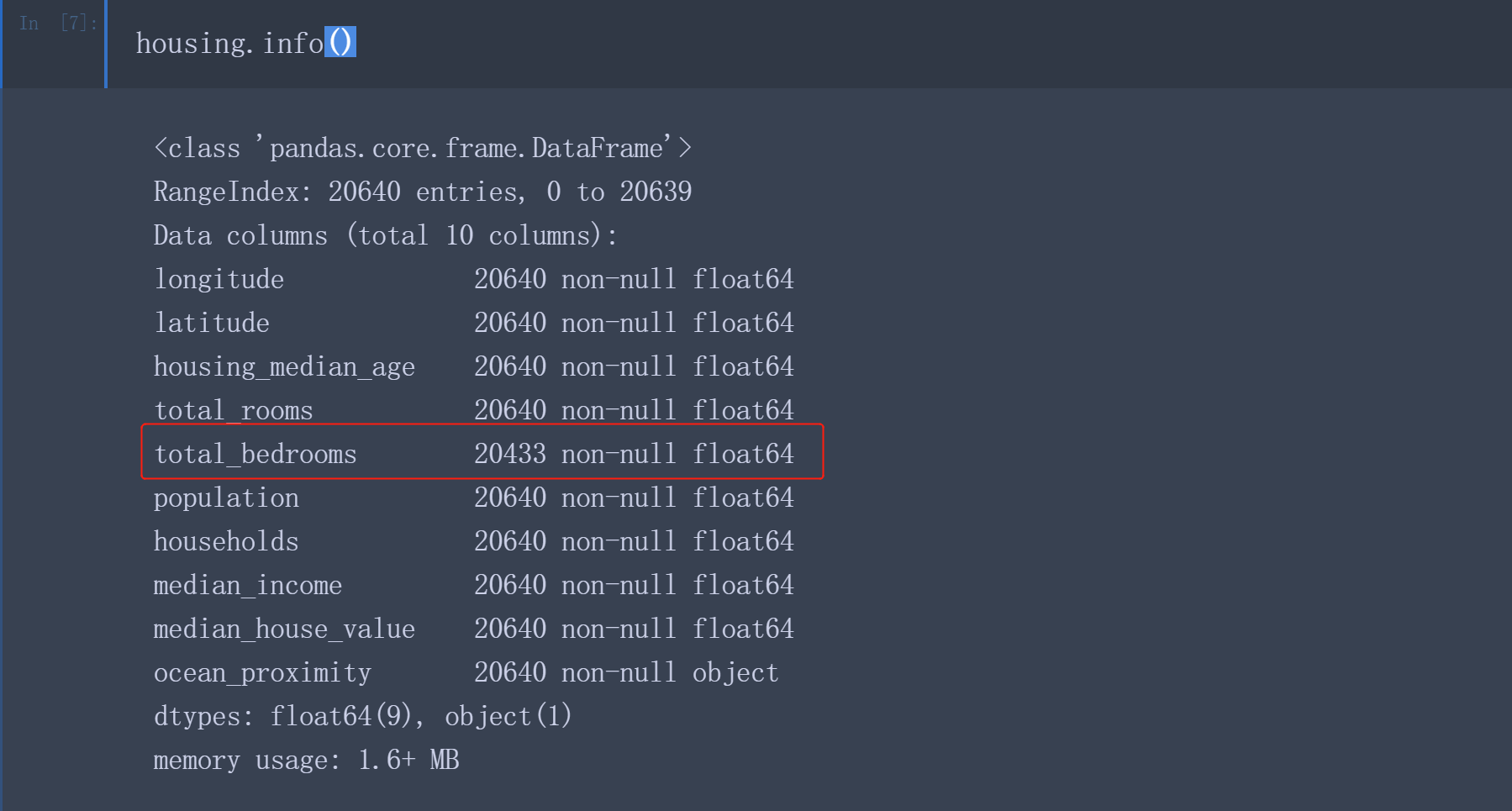
在这里插入图片描述
数据集中包含20640个实例， total_bedrooms这个属性只有20433个非空值，这意味着有207个区域缺失这个特征。我们后面需要考虑到这一点。
所有属性的字段都是数字，除了ocean_proximity，其类型是object。之前通过head()方法查看前五行，发现该列中的值是重复的，表明它有可能是一个分类属性，采用value_counts()方法查看由多少种分类存在，每种类别下分别有多少个区域。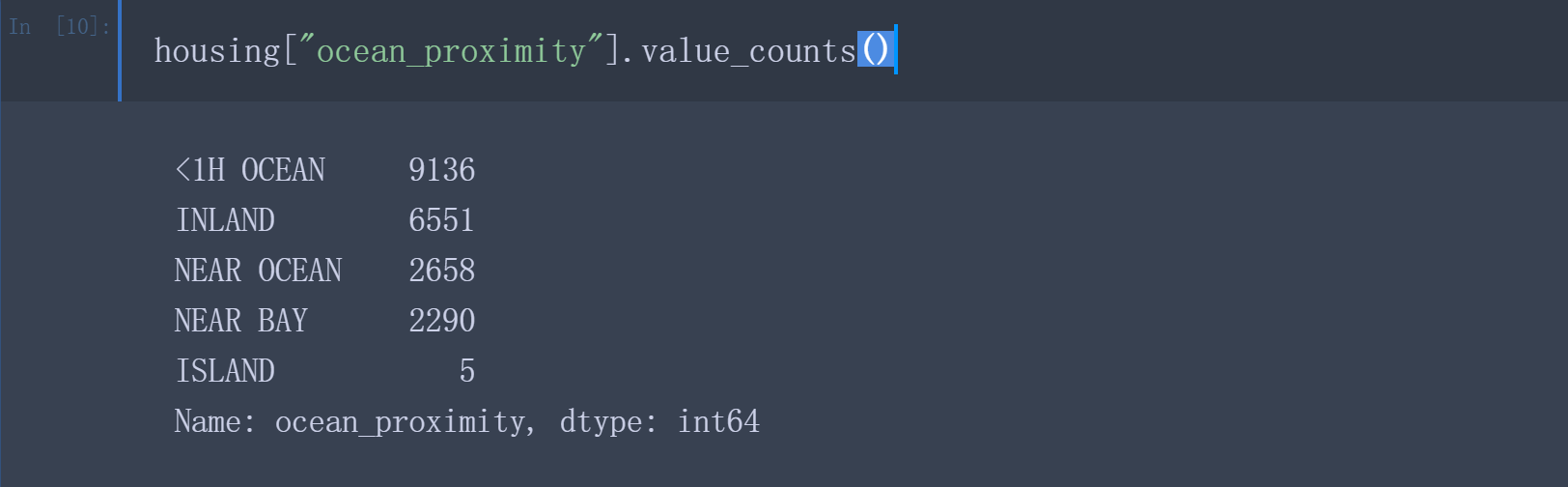
在这里插入图片描述
利用describe()方法可以显示数值属性的摘要。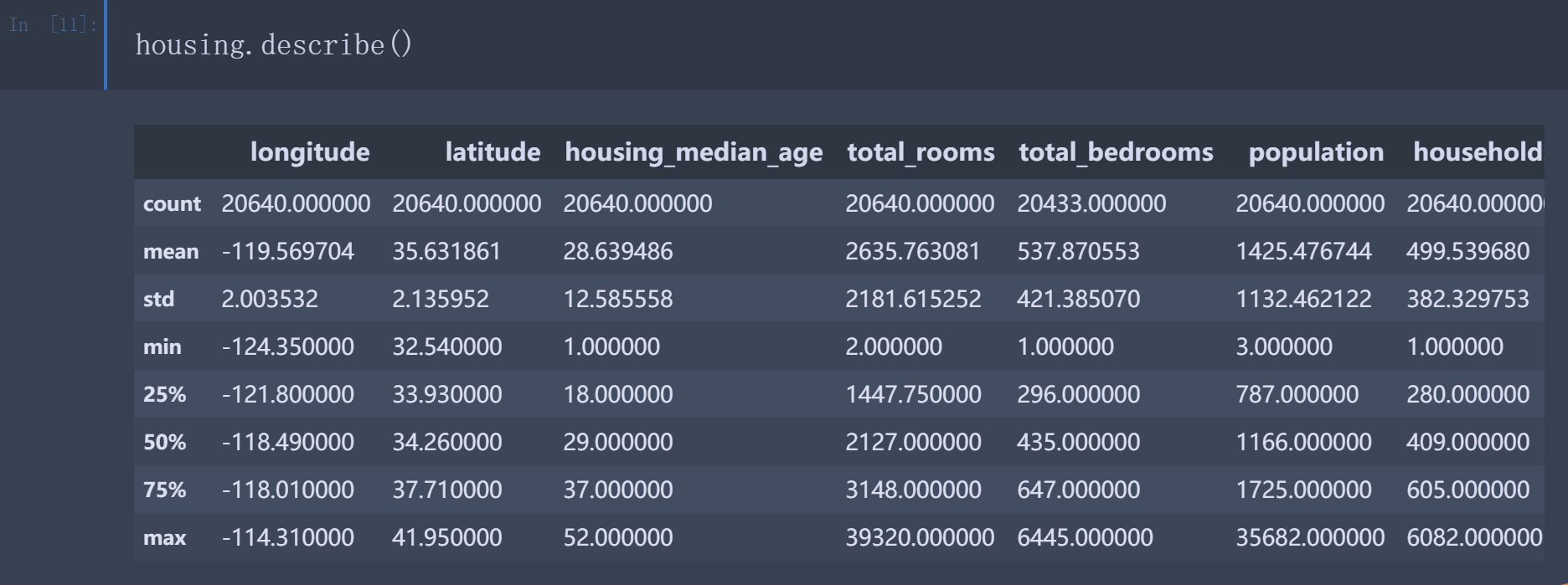
在这里插入图片描述
count：非空值计数
mean：平均值
std：标准差
min：最小值
25%、50%、75%：表示一组观测值中给定百分比的观测值都低于该值。例如， 对于housing_median_age的值， 25%的区域低于18， 50%的区域低于29， 以及75%的区域低于
37。

另外一种快速了解数据类型的方法是绘制每个数值属性的直方图。直方图用来显示给定范围（横轴）的实例数量（纵轴）。

1
2
3
4
%matplotlib inline # only in a Jupyter notebook
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
plt.show()
创建测试集

理论上创建测试机非常简单：只需要随机选择一些实例，通常是数据集的20%，然后将它们放在一边。

1
2
3
4
5
6
7
8
9
10
11
#np.random.seed(42)
import numpy as np
# For illustration only. Sklearn has train_test_split()
def split_train_test(data, test_ratio):
    shuffled_indices = np.random.permutation(len(data))
    test_set_size = int(len(data) * test_ratio)
    test_indices = shuffled_indices[:test_set_size]
    train_indices = shuffled_indices[test_set_size:]
    return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_train_test(housing, 0.2)
print(len(train_set), "train +", len(test_set), "test")

如果这样，再运行一遍，又会产生一个不同的数据集。通常的解决方案是在第一次运行程序后随即保存测试机，之后只是加载它而已。另一种方法是在调用np.random.permutation()之前设置一个随机数生成器的种子np.random.seed(42)，从而让它始终生成相同的随机索引。
但是，这两种解决方案在下一次获取更新的数据时都会中断。常见的解决办法是每个实例都使用一个标识符（identifier）来决定是否进入测试集（假定每个实例都有一个唯一且不变的标识符）。举例来说，你可以计算每个实例标识符的hash值，只取hash的最后一个字节，如果该值小于等于51（约256的20%），则将该实例放入测试集。这样可以确保测试集在多个运行里都是一致的，即便更新数据集也仍然一致。新实例的20%将被放入新的测试集，而之前训练集中的实例也不会被放入新测试集。实现方式如下：

1
2
3
4
5
6
7
8
9
import hashlib

def test_set_check(identifier, test_ratio, hash):
    return hash(np.int64(identifier)).digest()[-1] < 256 * test_ratio

def split_train_test_by_id(data, test_ratio, id_column, hash=hashlib.md5):
    ids = data[id_column]
    in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio, hash))
    return data.loc[~in_test_set], data.loc[in_test_set]

这里housing数据集没有标识符列，最简单的办法是使用行索引作为ID：

1
2
housing_with_id = housing.reset_index() # adds an `index` column
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")

同时Scikit-Learn提供了一些函数， 可以通过多种方式将数据集分成多个子集。 最简单的函数是train_test_split， 它与前面定义的函数split_train_test几乎相同， 除了几个额外特征。 首先， 它也有random_state参数， 让你可以像之前提到过的那样设置随机生成器种子； 其次， 你可以把行数相同的多个数据集一次性发送给它， 它会根据相同的索引将其拆分（例如， 当你有一个单独的DataFrame用于标记时， 这就非常有用） ：

1
2
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)

从数据探索和可视化中获得洞见

在这个问题中，由于存在地理位置信息（经纬度），因此可建立一个各区域的分布图便于数据可视化。

1
2
3
housing = strat_train_set.copy()
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
save_fig("better_visualization_plot")

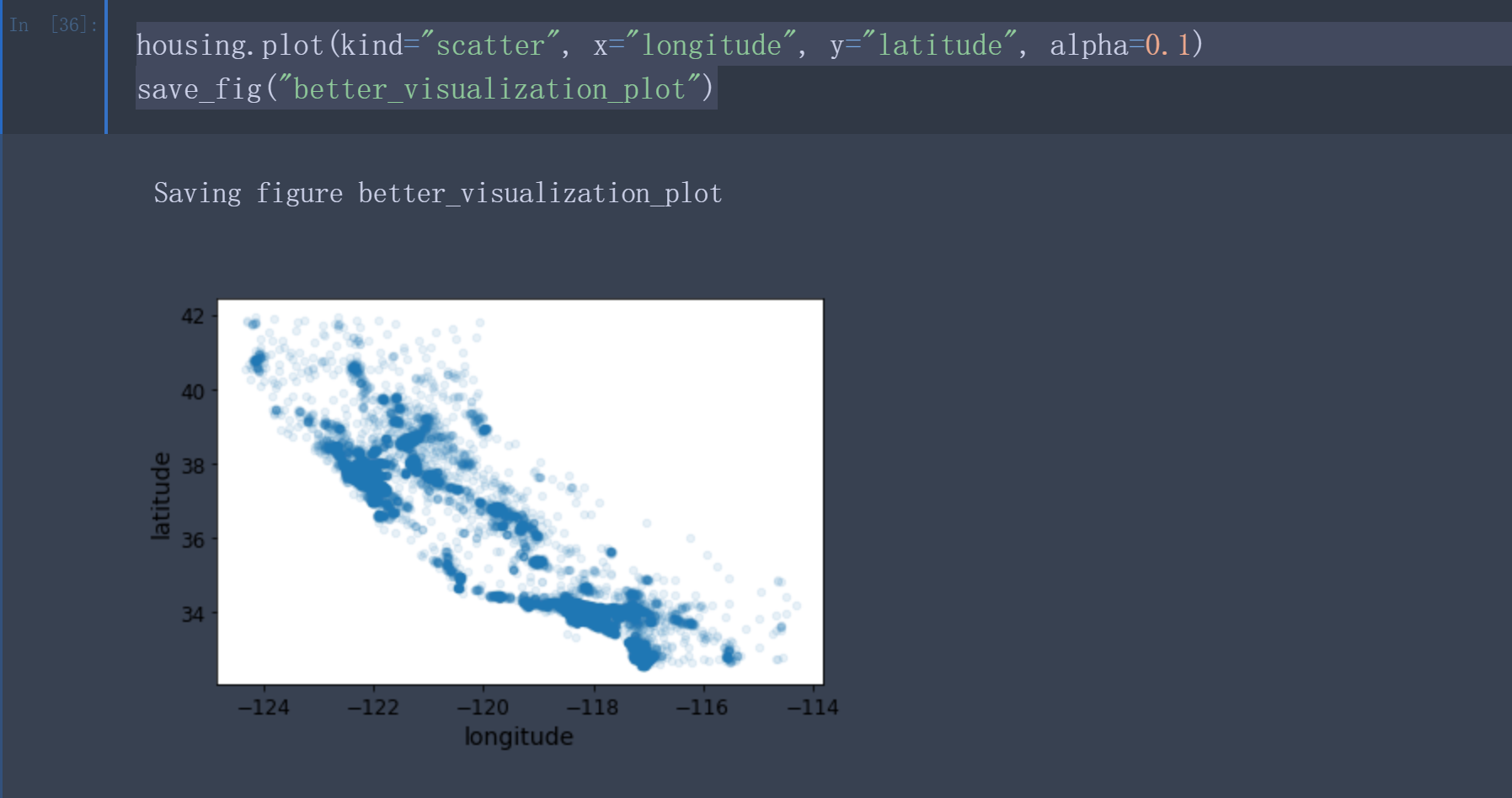
在这里插入图片描述
现在，再来看看房价。每个圆的半径大小代表了每个地区的人口数量（选项s） ， 颜色代表价格（选项c） 。 我们使用一个名叫jet的预定义颜色表（选项cmap） 来进行可视化， 颜色范围从蓝（低） 到红（高） ： 

1
2
3
4
5
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population",
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
)p
lt.legend()

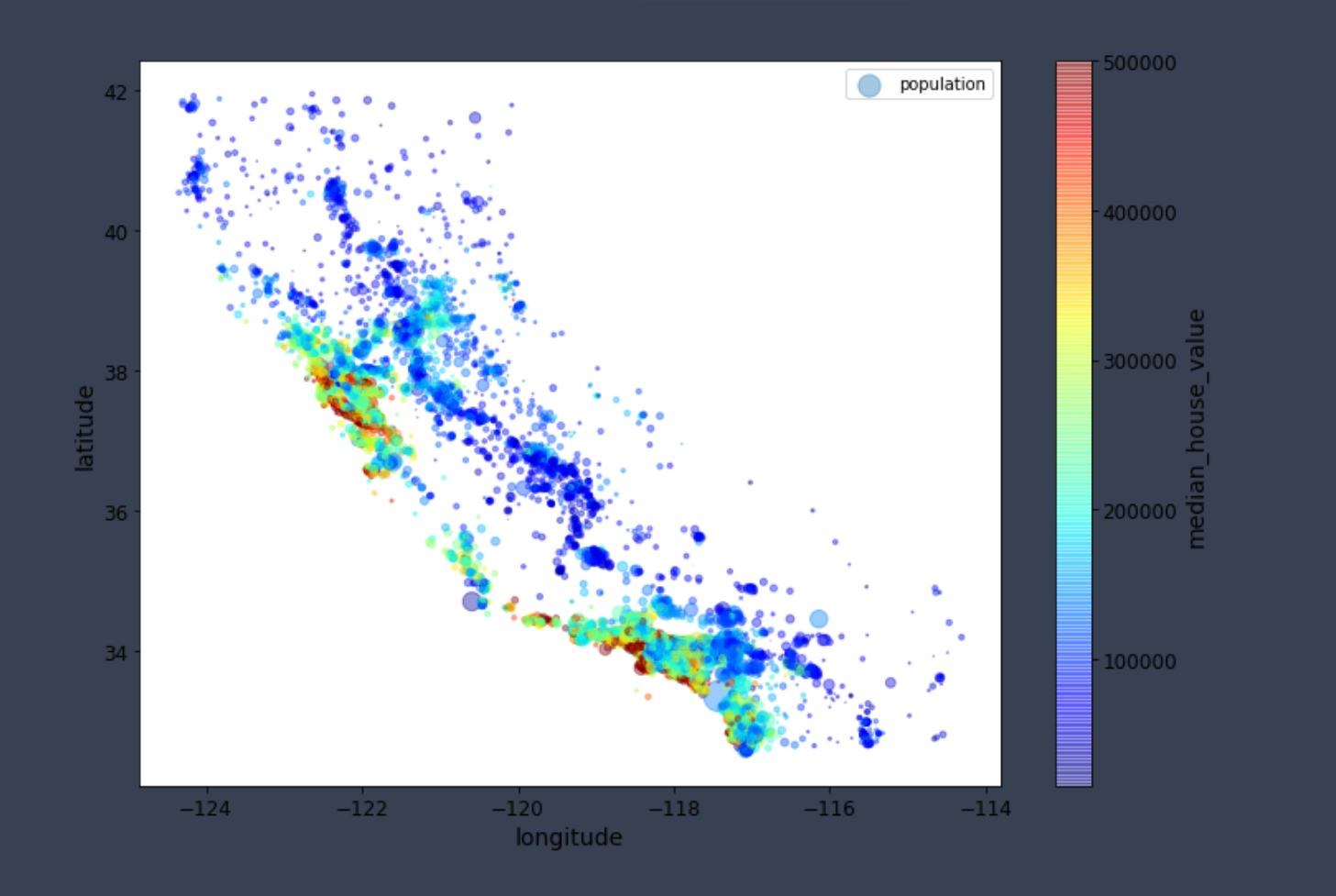在这里插入图片描述　　这张图片告诉你房屋价格与地理位置（例如靠海）和人口密度息息相关，这点你可能早已知晓。一个通常很有用的方法是，使用聚类算法来检测主群体，然后再为各个聚类中心添加一个新的衡量邻近距离的特征。

寻找相关性

由于数据集不大，你可以使用corr（）方法轻松计算出每对属性之间的标准相关系数
得到每个属性与房屋中位数的相关性分别是：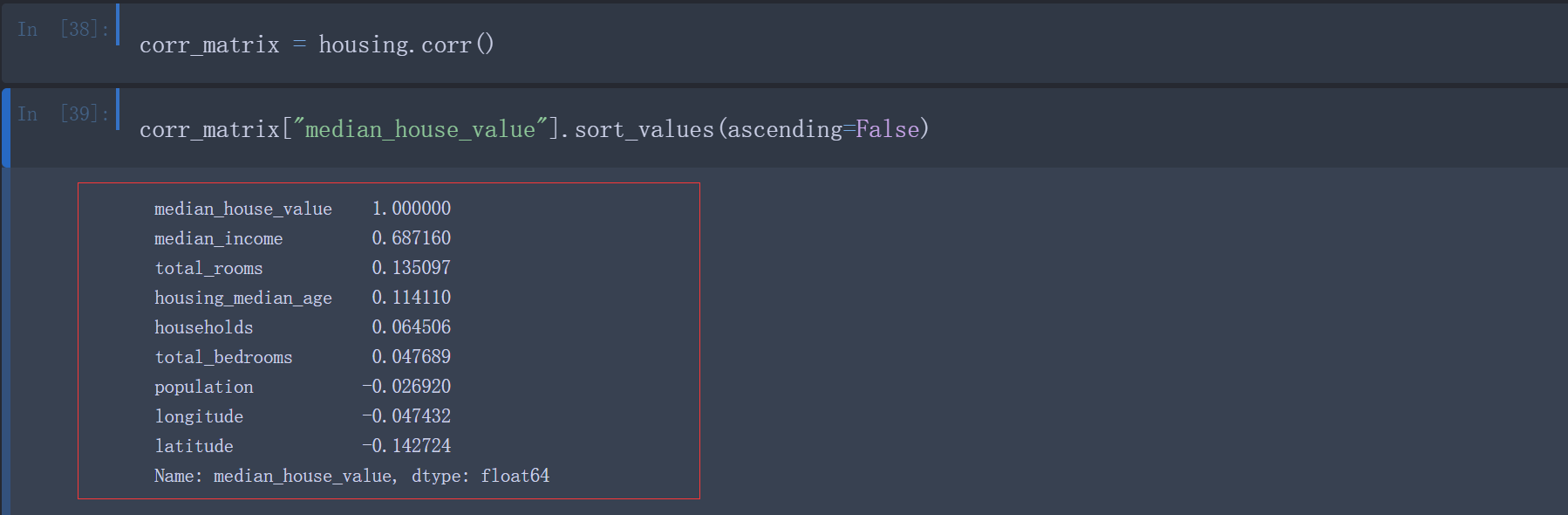
在这里插入图片描述
相关系数的范围从-1变化到1。 越接近1， 表示有越强的正相关； 当系数接近于-1， 则表示有强烈的负相关； 注意看纬度和房价中位数之间呈现出轻微的负相关（也就是说， 越往北走， 房价倾向于下降） 。 最后， 系数靠近0则说明二者之间没有线性相关性。

机器学习算法的数据准备

让我们先回到一个干净的数据集（再次复制strat_train_set），然后将预测器和标签分开，因为这里我们不一定对它们使用相同的转换方式（需要注意drop（）会创建一个数据副本，但是不影响strat_train_set）：

1
2
housing = strat_train_set.drop("median_house_value", axis=1)#strip() 方法用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列。默认删除行，axis=1表示删除列
housing_labels = strat_train_set["median_house_value"].copy()#拷贝median_house_value作为label
数据清理

针对前面提到的total_bedrooms属性有部分值缺失，可以采用以下选择：

  • 放弃这些响应的地区
  • 放弃这个属性
  • 将缺失的值设置为某个值（0、平均数或者中位数等都可以）
1
2
3
4
housing.dropna(subset=["total_bedrooms"]) # option 1 dropna删除指定列中包含缺失值的行
housing.drop("total_bedrooms", axis=1) # option 2
median = housing["total_bedrooms"].median() #计算中位值
housing["total_bedrooms"].fillna(median) # option 3

Scikit-Learn提供了一个非常容易上手的教程来处理缺失值：imputer。
下面是其使用方法：首先，需要创建一个Imputer实例，指定用该属性的中位数替换它的每个缺失值：

1
2
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy="median")

由于中位数值只能在数值属性上计算， 所以我们需要创建一个没有文本属性的数据副本ocean_proximity：

1
housing_num = housing.drop("ocean_proximity", axis=1)

使用fit（） 方法将imputer实例适配到训练集:

1
imputer.fit(housing_num)

imputer计算出了每个属性的中位数，并将结果保存在了实例变量statistics_中。只有属性total_bedrooms有缺失值，但是我们要确保一旦系统运行起来，新的数据中没有缺失值，所以安全的做法是将imputer应用到每个数值：
在这里插入图片描述)在这里插入图片描述
现在，你就可以使用这个“训练过的”imputer来对训练集进行转换，通过将缺失值替换为中位数：

1
X = imputer.transform(housing_num)

结果是一个普通的Numpy数组，包含有转换后的特征。如果你想将其放回到Pandas DataFrame中，也很简单：
housing_tr = pd.DataFrame(X, columns=housing_num.columns)

选择和训练模型

现在是时候选择机器学习模型并展开训练
在训练集上训练和评估

先训练一个线性回归模型

1
2
3
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)

完成后,现在就有了一个可用的线性回归模型。用一些训练集中的实例做以下验证：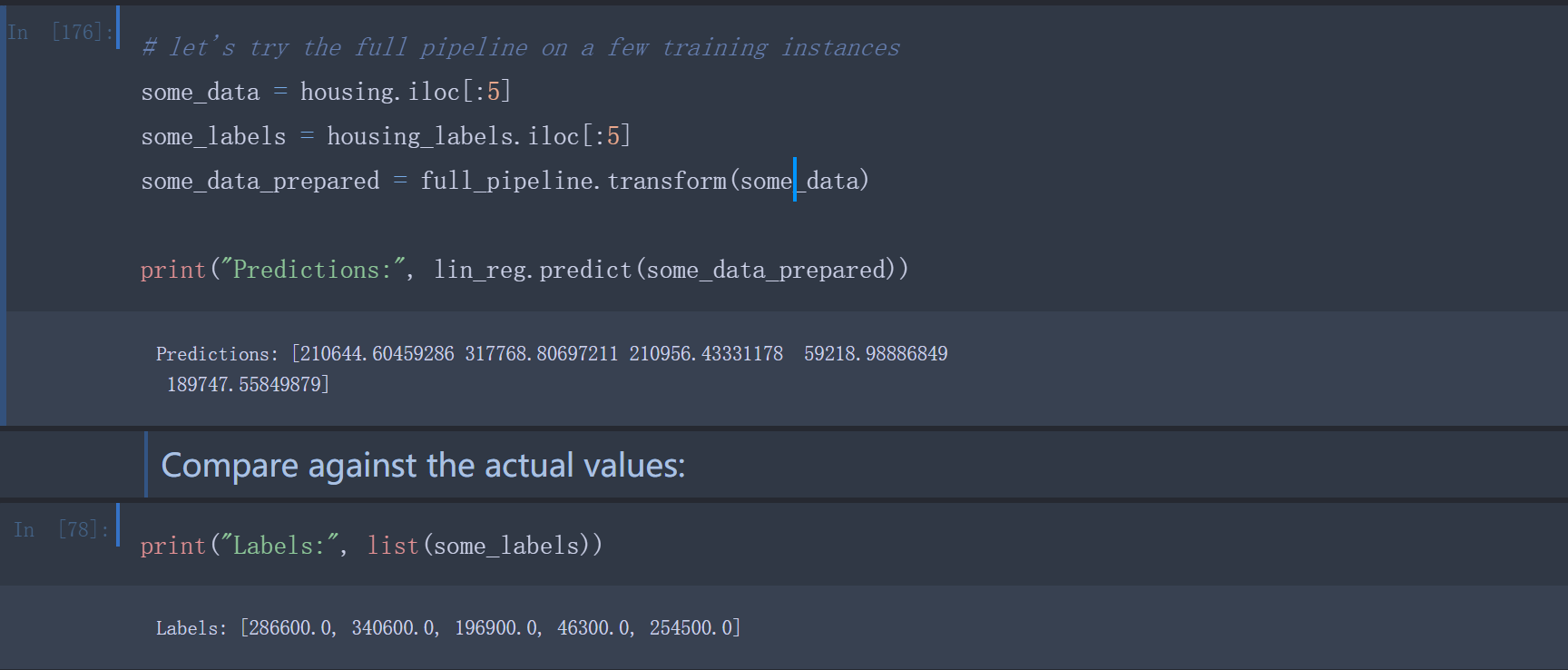
在这里插入图片描述
比较预测值与标签值，看准确率如何。还可以使用Scikit-Learn的mean_squared_error函数，计算该线性回归模型的RMSE均方根误差。

1
2
3
4
5
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse

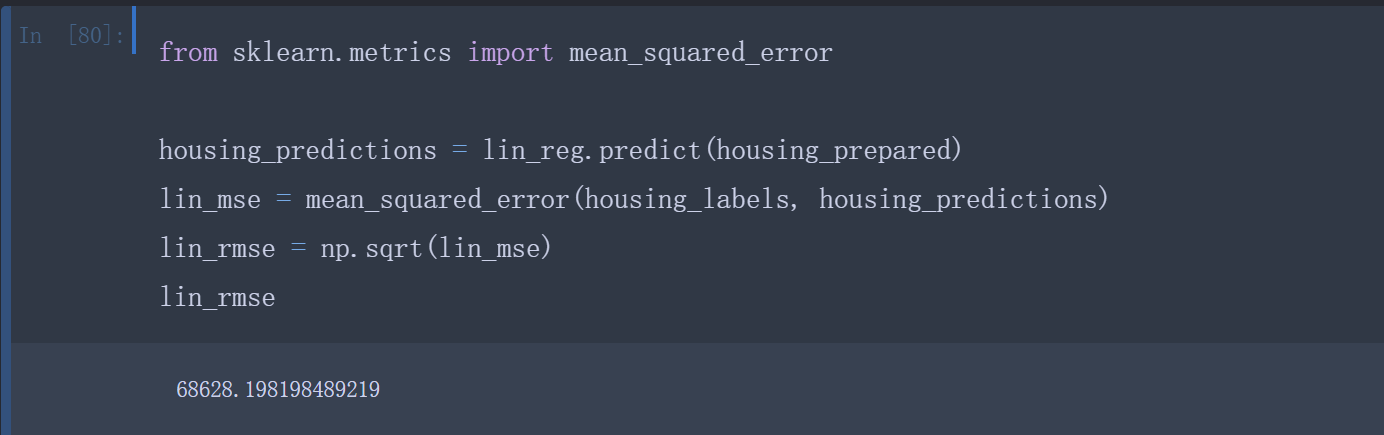
在这里插入图片描述
再来训练一个DecisionTreeRegressor决策树模型

1
2
3
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(random_state=42)
tree_reg.fit(housing_prepared, housing_labels)

训练完成后可以用训练集来评估一下

1
2
3
4
housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse

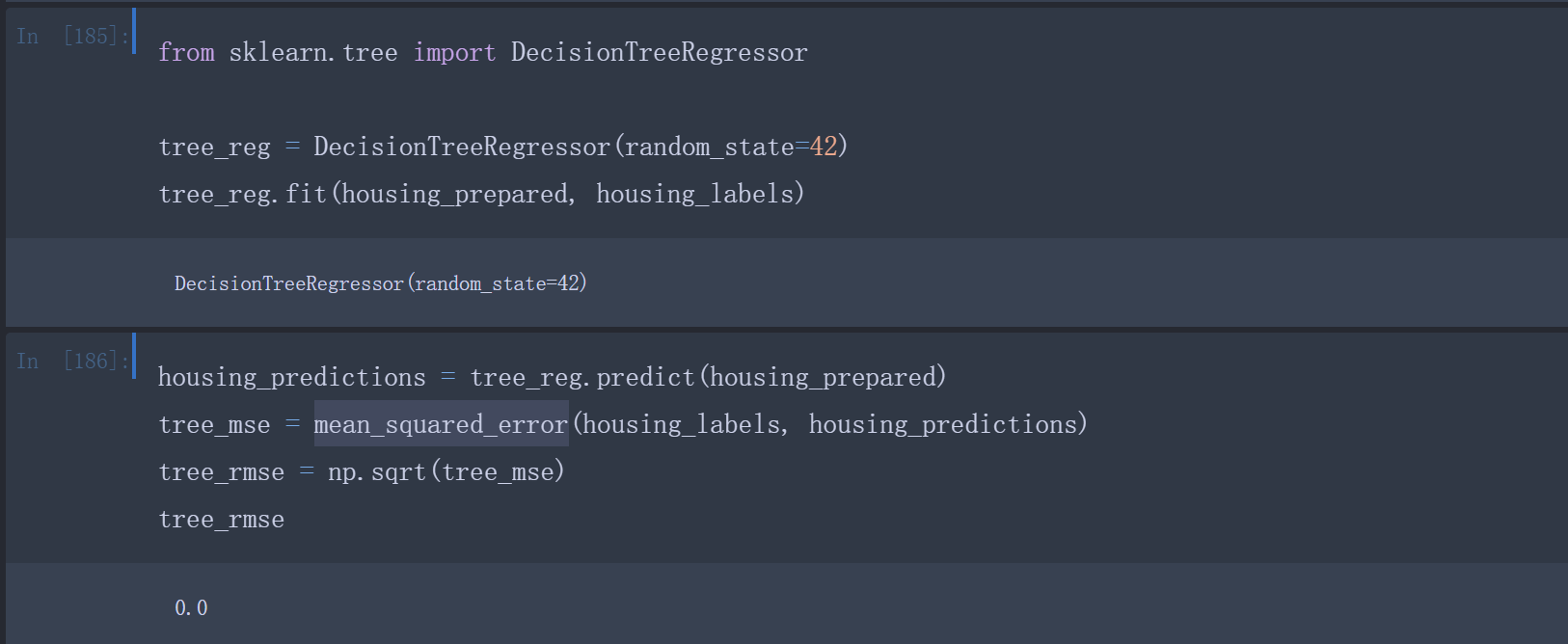
在这里插入图片描述
均方误差为0，可能是由于模型对数据严重过拟合了。

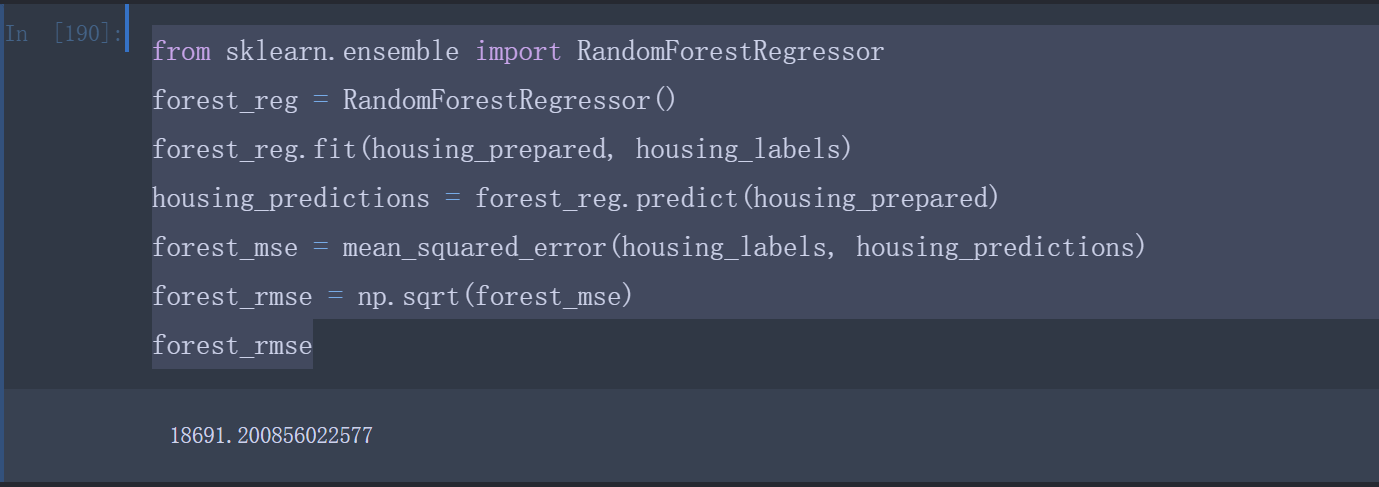
尝试最后一个模型：RandomForestRegressor 　　随机森林的工作原理是通过对特征的随机子集进行许多个决策树的训练，然后对其预测取平均。

1
2
3
4
5
6
7
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(housing_prepared, housing_labels)
housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels, housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse

在这里插入图片描述

微调模型

网格搜索

一种微调的方法是手动调整超参数，找到一组很好的超参数值组合。
还可以可以用Scikit-Learn的GridSearchCV来替你进行探索。你所要做的只是告诉GridSearchCV你要进行实验的超参数是什么，以及需要尝试的值，GridSearchCV将会使用交叉验证来评估超参数值的所有可能的组合。例如，下面这段代码搜索RandomForestRegressor的超参数值的最佳组合：

1
2
3
4
5
6
7
8
9
from sklearn.model_selection import GridSearchCV
param_grid = [
    {'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
    {'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
  ]
forest_reg = RandomForestRegressor()
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
                           scoring='neg_mean_squared_error')
grid_search.fit(housing_prepared, housing_labels)

当你不能确定超参数该有什么值，一个简单的方法是尝试连续的10的次方（如果想要一个粒度更小的搜寻，可以用更小的数，就像在这个例子中对超参数n_estimators做的）。

param_grid告诉Scikit-Learn首先评估所有的列在第一个dict中的n_estimators和max_features的3 × 4 = 12种组合（不用担心这些超参数的含义，会在第7章中解释）。然后尝试第二个dict中超参数的2 × 3 = 6种组合，这次会将超参数bootstrap设为False而不是True（后者是该超参数的默认值）。

总之，网格搜索会探索12 + 6 = 18种RandomForestRegressor的超参数组合，会训练每个模型五次（因为用的是五折交叉验证）。换句话说，训练总共有18 × 5 = 90轮！折将要花费大量时间，完成后，你就能获得参数的最佳组合，如下所示：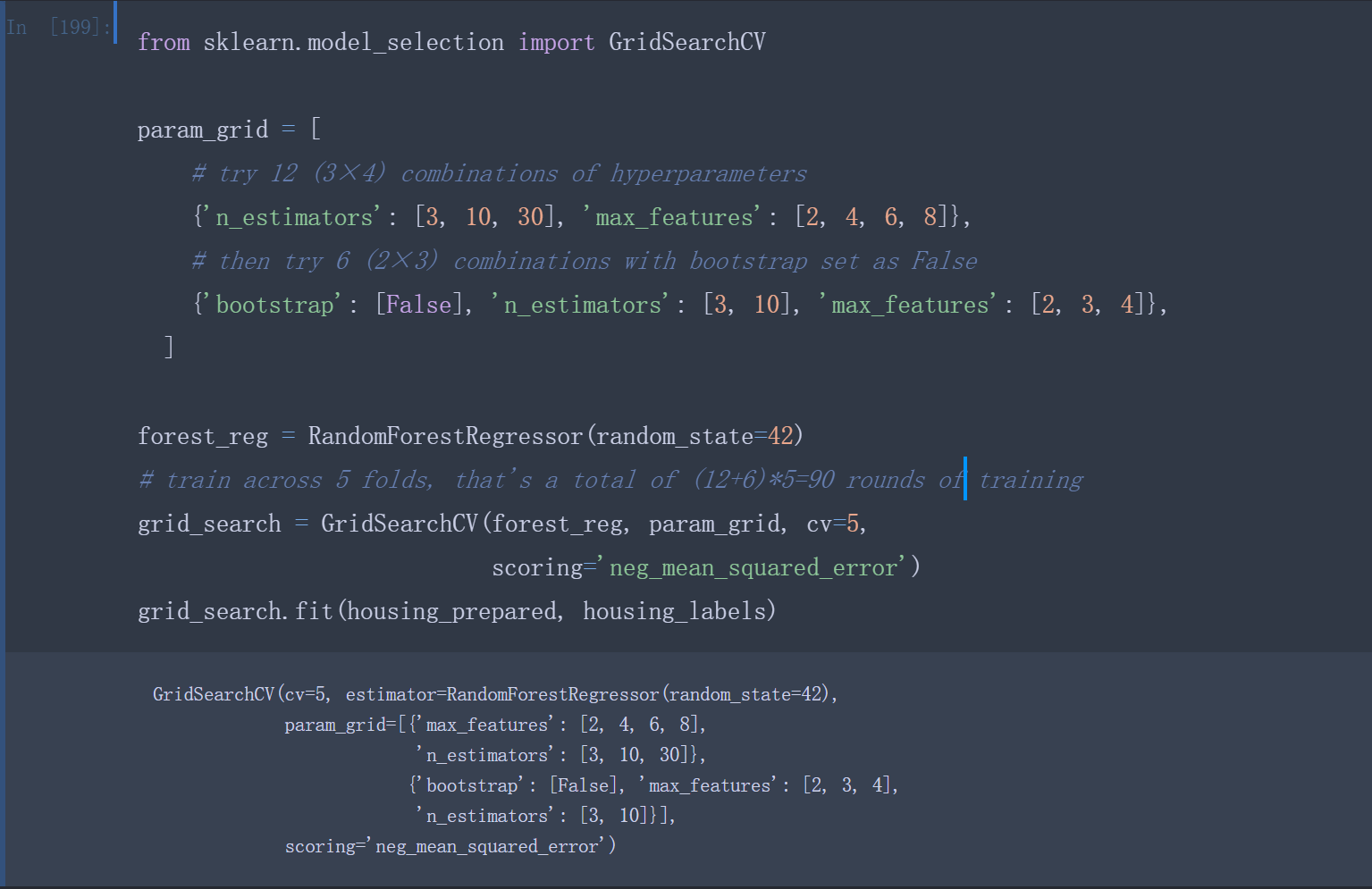
在这里插入图片描述
在这里插入图片描述

随机搜索

当探索相对较少的组合时，就像前面的例子，网格搜索还可以。但是当超参数的搜索空间很大时，最好使用RandomizedSearchCV。这个类的使用方法和类GridSearchCV很相似，但它不是尝试所有可能的组合，而是通过选择每个超参数的一个随机值的特定数量的随机组合。这个方法有两个优点：

  • 如果你让随机搜索运行，比如1000次，它会探索每个超参数的1000个不同的值（而不是像网格搜索那样，只搜索每个超参数的几个值）。

  • 你可以方便地通过设定搜索次数，控制超参数搜索的计算量。