Honor's Blog

爱笑的小土豆~

发表于 更新于 分类于

时域频域联合分析

这个例子说明如何使用交互式线性系统分析及应用程序并排比较多种类型的响应，包括时域和频域响应。
创建一个想要比较其响应的模型，如比较一个三阶模型G和G与两个不同控制器C1和C2的闭环响应。

阅读全文 »

发表于 更新于 分类于

Vector

vector是线性容器，可叫做“变长数组”，即“长度可根据需要而自动改变的数组”调整存储空间大小。它的元素存储在一块连续的存储空间中，可以使用迭代器iterator和指针的偏移地址访问元素。

1.vector的定义

单独定义一个vector：vector<typename> name;
这个定义相当于是一维数组name[SIZE],不过长度可以根据需要进行变化，比较节省空间。
typename可以是任何基本类型，例如int,double、char、结构体等，也可以是STL标准容器，例如vector、set、queue等。
如果typename是vector，可以按下面这样定义：
vector<vector<int> > name;

2.vector容器内元素的访问

（1）通过下标访问
和访问普通数组是一样，对一个定义为vector vec的vector容器来说，直接访问vec[index]（如vec[0]、vec[1]),这里的下标是从0到vec.siz()-1.
（2）通过迭代器访问
迭代器（iterator）定义：
vector<typename>::iterator it;
可以将迭代器理解为一种类似指针的东西。
可通过类似下表和指针访问数组的方式来访问容器内的元素：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<cstdio>
#include<vector>
using namespace std;
int main()
{
    vector<int> vec; 
    for(int i=1;i<=5;i++)
    {
        vec.push_back(i);
    }
    vector<int>::iterator it=vec.begin();//vec.begin()为取vec的首元素地址，it指向这个地址
/* 另一种遍历vector中元素的写法：
for(vector<int>::iterator it=vec.begin();it!=vec.end();it++)
*/
    for(int i=0;i<5;i++)
    {
        printf("%d ",*(it+i));
    }
    return 0;
}siz

vec[i]和*(vec.begin()+i)是等价的。

3.vector常用函数
  1. push_back(x),在vector后面添加一个元素x。
  2. pop_back(),删除vector的尾元素。
  3. size()，获取vector中元素的个数
  4. clear()，清空vector中的所有元素，时间复杂度为O(N),其中N为vector中元素的个数。
  5. insert(),插入元素到某个位置中，insert(iterator loc，x)用来向vector的指定位置loc前插入一个元素x。
  6. erase(),有两种用法:删除单个元素，删除一个区间内的所有元素。erase(it)删除迭代器为it处的元素，earse(first,last)删除[first,last)内的所有元素。
    empty(),表示判断vector是否为空，如果为空，则返回true.
    容器的大小和容器的容量是有区别的，大小 是指元素的个数，容量是分配的内存大小，容量一般不小于容器的大小。vector::size()返回容器的大小，vector::capacity()返回容量值。
    vector的特点如下:
  • 随机访问元素效率很高
  • push_back的效率也会很高
  • push_front的效率非常低，不建议使用
  • vector在末尾添加和删除元素相对较好，而在其他位置添加和删除元素则不及其他顺序容器，在迭代器和引用也没有list支持的好

String

  1. string的定义
    定义string的方式跟基本数据类型相同，只需要在stirng后面跟上变量名，string str;，初始化可以海子街给string类型的变量赋值。
    string str="abcd";

  2. string中内容的访问：
    (1)可以直接通过下标访问，str[i]
    (2)通过迭代器访问,string::iterator it;

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    #include<iostream>
    #include<string>
    using namespace std;
    int main()
    {
        string str="abcd";
        for(string::iterator it=str.begin();it!=str.end();it++)
        {
            cout<<*it;
        }
        return 0;
    }

    string和vector一样，可以直接对迭代器进行加减某个数字，如str.begin()+3

  3. 常用函数实例

  4. 两个string可以直接通过+拼接起来。

  5. 两个string类型可以直接使用==、!=、<、<=、>、>=比较大小，比较规则是字典序。(比较两个字符串对应的ASCII码值)

  6. length()/size()，length()返回string的长度，即存放的字符数，时间复杂度为O(1)。

  7. insert()

  8. erase()
    两种用法:删除单个元素，删除一个区间内的所有元素。
    str.erase(it)用于删除单个元素，it为需要删除的元素的迭代器。

string类的构造函数：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
string str：生成空字符串

string s(str)：生成字符串为str的复制品

string s(str, strbegin,strlen)：将字符串str中从下标strbegin开始、长度为strlen的部分作为字符串初值

string s(cstr, char_len)：以C_string类型cstr的前char_len个字符串作为字符串s的初值

string s(num ,c)：生成num个c字符的字符串

string s(str, stridx)：将字符串str中从下标stridx开始到字符串结束的位置作为字符串初值

eg:


    string str1;               //生成空字符串
    string str2("123456789");  //生成"1234456789"的复制品
    string str3("12345", 0, 3);//结果为"123"
    string str4("012345", 5);  //结果为"01234"
    string str5(5, '1');       //结果为"11111"
    string str6(str2, 2);      //结果为"3456789"

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
#include <string>
using namespace std;
int main()
{
    string str1;               //生成空字符串
    string str2("123456789");  //生成"1234456789"的复制品
    string str3("12345", 0, 3);//结果为"123"
    string str4("0123456", 5);  //结果为"01234"
    string str5(5, '1');       //结果为"11111"
    string str6(str2, 2);      //结果为"3456789"
    cout<<"str2:"<<str2<<endl;
    cout<<"str3:"<<str3<<endl;
    cout<<"str4:"<<str4<<endl;
    cout<<"str5:"<<str5<<endl;
    cout<<"str6:"<<str6<<endl;
    return 0;
}

输出结果：
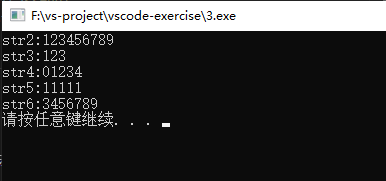
在这里插入图片描述

string的大小和容量
  1. size()和length()：返回string对象的字符个数，它们执行效果相同。
  2. max_size()：返回string对象最多包含的字符数，超出会抛出length_error异常
  3. capacity()：重新分配内存之前，string对象能包含的最大字符数
string的大小写转换:tolower()和toupper()函数 或者 STL中的transform算法

方法一：使用C语言的函数，进行转换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>
#include <string>
using namespace std;

int main()
{
    string str = "ABCDEFG";

    for( int i = 0; i < str.size(); i++ )
    {
        str[i] = tolower(str[i]);
    }

    cout<<str<<endl;
    return 0;
}
to_string 将数值转换为字符串，返回对应的字符串
1
2
3
4
5
6
7
8
9
10
11
12
#include <iostream>   
#include <string>     
using namespace std;
 
int main ()
{
  string pi = "pi is " + std::to_string(3.1415926);
  string perfect = std::to_string(1+2+4+7+14) + " is a perfect number";
  cout << pi << '\n';
  cout << perfect << '\n';
  return 0;
}

结果：
pi is 3.141593
28 is a perfect number

set

set，是一个内部自动有序且不含重复元素的容器。set作为一个容器是用来存储同一数据类型的数据类型，并且能从一个数据结合中取出数据，在set中每个元素的值都是唯一的，

set常用函数实例
1.insert(x)
可将x插入set容器中，并自动递增排序和去重，时间复杂度为O(logN),其中N为set内的元素个数。
2.find()
find(value)返回set中对应值为value的迭代器，时间复杂度为O(logN)，N为set内的元素个数。
3.erase()

  • 删除单个元素:
    st.erase(it),it为需要删除元素的迭代器，时间复杂度为O(1)。可结合find()函数一起使用
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    #include<iostream>
    #include<set>
    using namespace std;
    int main()
    {
        set<int> st;
        st.insert(100);
        st.insert(200);
        st.insert(100);
        st.insert(300);
        st.erase(st.find(100));//先利用find()函数找到100，然后用erase删除它
        st.erase(st.find(200));
        for(set<int>::iterator it=st.begin();it!=st.end();it++)
        {
            cout<<*it;
        }
        return 0;
    }
    st.erase(value)，其中value为需要删除元素的值。时间复杂度为O(logN)。
  • 删除一个区间内的所有元素
    st.erase(first,last)可以删除一个区间内的所有元素，其中first为所需要删除区间的起始迭代器，last为待删除区间的末尾迭代器的下一个地址，即为删除[first,last].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<iostream>
#include<set>
using namespace std;
int main()
{
    set<int> st;
    st.insert(20);
    st.insert(10);
    st.insert(40);
    st.insert(30);
    set<int>::iterator it=st.find(30);
    st.erase(it,st.end()); //删除元素30至set末尾之间的元素，即30和40
    for(set<int>::iterator it=st.begin();it!=st.end();it++)
    {
        cout<<*it<<' ';
    }
    return 0;
}

4.size()
用来获取set内元素的个数，时间复杂度为O(1)。
5. clear()
清空set内的所有元素，复杂度为O(N),其中N为set内元素的个数

map

map本质是一个关联式容器，它提供一对一的hash。里面的数据都是成对出现的：

  • 每一对中的第一个值称为关键字(key），每个关键字只能在map中出现一次；
  • 第二个称为该关键字的值(value)。
    map以模板(泛型)方式实现，可以存储任意类型的数据，包括使用者自定义的数据类型。map主要用于资料一对一映射(one-to-one)的情況，map內部的实现自建一颗红黑树(一种非严格意义上的平衡二叉树)，这颗树具有对数据自动排序的功能。在map内部所有的数据都是有序的，后边我们会见识到有序的好处。
    map可自动简历key-value的一一对应关系，比如一个班级中，每个学生的学号跟他的姓名就存在着一一映射的关系。

1.插入元素
map的插入有3种方式：用insert函数插入pair数据，用insert函数插入value_type数据和用数组方式插入数据。
第一种：用insert函数插入pair数据

1
2
map<int, string> mapStudent;
mapStudent.insert(pair<int, string>(1,“student_one”));

第二种：用insert函数插入value_type数据

1
2
map<int, string> mapStudent;
mapStudent.insert(map<int, string>::value_type (1,"student_one"));

用make_pair

1
mapStudent.insert(make_pair(1, "student_one"));

第三种：用数组方式插入数据

1
2
3
map<int, string> mapStudent;
mapStudent[1] = “student_one”;
mapStudent[2] = “student_two”;

以上四种用法，虽然都可以实现数据的插入，但是它们是有区别的，当然了第一种和第二种在效果上是完成一样的，用insert函数插入数据，在数据的插入上涉及到集合的唯一性这个概念，即当map中有这个关键字时，insert操作是不能再插入这个数据的，但是用数组方式就不同了，它可以覆盖以前该关键字对应的值,即：如果当前存在该关键字，则覆盖改关键字的值，否则，以改关键字新建一个key—value;
2.查找元素
用find函数来定位数据出现位置，它返回的一个迭代器，当所查找的关键字key出现时，它返回数据所在对象的位置，如果沒有，返回迭代器等于end函数返回的迭代器。

1
2
3
4
5
6
7
8
// find 返回迭代器指向当前查找元素的位置否则返回map::end()位置
iter = mapStudent.find("123456");
 
if(iter != mapStudent.end())
       cout<<"Find, the value is"<<iter->second<<endl;
else
   cout<<"Do not Find"<<endl;

3.删除与清空元素

1
2
3
4
5
6
7
8
9
10
//迭代器刪除
iter = mapStudent.find("123");
mapStudent.erase(iter);
 
//用关键字刪除
int n = mapStudent.erase("123"); //如果刪除了会返回1，否则返回0
 
//用迭代器范围刪除 : 把整个map清空
mapStudent.erase(mapStudent.begin(), mapStudent.end());
//等同于mapStudent.clear()

4.map的大小
在往map里面插入了数据，我们怎么知道当前已经插入了多少数据呢，可以用size函数，用法如下：
int nSize = mapStudent.size();
5.map的基本操作函数
C++ maps是一种关联式容器，包含“关键字/值”对

begin() 返回指向map头部的迭代器

clear() 删除所有元素

count() 返回指定元素出现的次数

empty() 如果map为空则返回true

end() 返回指向map末尾的迭代器

equal_range() 返回特殊条目的迭代器对

erase() 删除一个元素

find() 查找一个元素

get_allocator() 返回map的配置器

insert() 插入元素

key_comp() 返回比较元素key的函数

lower_bound() 返回键值>=给定元素的第一个位置

max_size() 返回可以容纳的最大元素个数

rbegin() 返回一个指向map尾部的逆向迭代器

rend() 返回一个指向map头部的逆向迭代器

size() 返回map中元素的个数

swap() 交换两个map

upper_bound() 返回键值>给定元素的第一个位置

value_comp() 返回比较元素value的函数

发表于 更新于 分类于

深度学习三个步骤：

  • 建立模型
    • 选择什么样的网络结构
    • 选择多少层，每层选择多少神经元
  • 损失函数
    • 选择常用损失函数，平方误差，交叉熵…..
  • 参数学习
    • 梯度下降
    • 反向传播算法

全连接神经网络DNN由于模型结构不够灵活，模型参数太多，通过模型改进，就出现了卷积神经网络CNN。
CNN在结构上有三大特性:

  1. 局部连接，在我们进行图像识别的时候，不需要对整个图像进行处理，只需要关注图像中某些特殊的区域，一张640x480的图片，可能其中的16x16个像素

  2. 权重共享

  3. 下采样，减小图片的尺寸，
    可以减少网络参数，加快训练速度。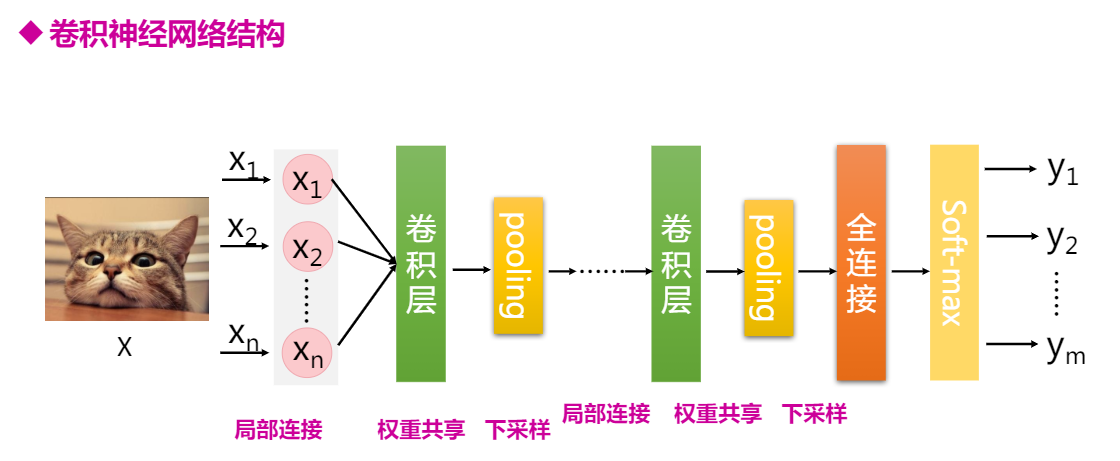
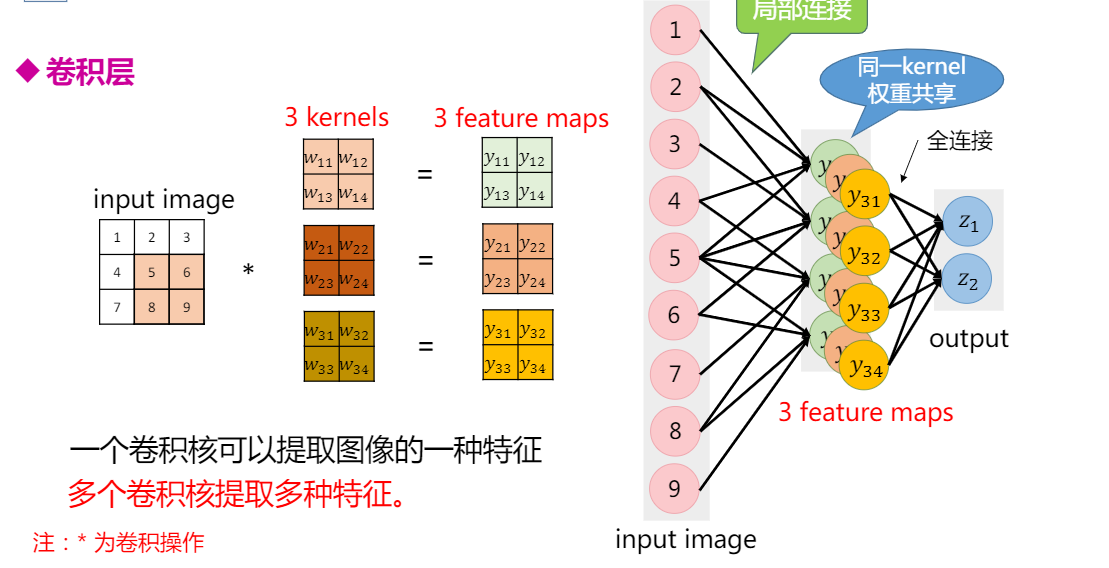
    在这里插入图片描述)在这里插入图片描述
    Pooling 池化层
    通过下采样缩减feature map尺度。常用maxpooling和averagepooling.

    卷积神经网络的一般结构

    1. 卷积层+激活层和池化层的组合多次出现，用来提取特征
    2. 多个全连接或特殊的CNN结构作为输出层，用作分类器/检测器/分割器

      经典的CNN结构

      在这里插入图片描述

      AlexNet

      在这里插入图片描述
      在这里插入图片描述

      VGG

      在这里插入图片描述
      在这里插入图片描述
      在AlexNet中用到一些非常大的卷积核，比如11x11、5x5的，感受野越大，看到的图片信息就越多，获得的特征会越好。但是随着参数和计算量的增加，如何衡量该使用多大的卷积核呢
      Methods:学习到使用2个3x3的卷积核的组合比仅使用1个5x5的卷积核效果更佳，并且参数量降低。
      在这里插入图片描述

这几天参加了百度飞桨举办的深度学习7日入门-CV疫情特辑课程，通过几个疫情AI实战案例，轻松入门深度学习。

Day01 新冠疫情可视化

利用python爬取丁香园公开的统计数据，根据累计确诊数，使用pyecharts绘制疫情分布图，通过查阅Pycharts api比较容易实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import json
import datetime
from pyecharts.charts import Pie
from pyecharts import options as opts

# 读原始数据文件
today = datetime.date.today().strftime('%Y%m%d')   #20200315
datafile = 'data/'+ today + '.json'
with open(datafile, 'r', encoding='UTF-8') as file:
    json_array = json.loads(file.read())

# 分析全国实时确诊数据：'confirmedCount'字段
china_data = []
for province in json_array:
    china_data.append((province['provinceShortName'], province['confirmedCount']))
china_data = sorted(china_data, key=lambda x: x[1], reverse=True)                 #reverse=True,表示降序，反之升序

print(china_data)
# 全国疫情地图
# 自定义的每一段的范围，以及每一段的特别的样式。

labels = [data[0] for data in china_data]
counts = [data[1] for data in china_data]

m = Pie()
m.add("", [list(z) for z in zip(labels, counts)])

#系列配置项,可配置图元样式、文字样式、标签样式、点线样式等
m.set_series_opts(label_opts=opts.LabelOpts(formatter="{b}: {c}")
            )
#全局配置项,可配置标题、动画、坐标轴、图例等
m.set_global_opts(title_opts=opts.TitleOpts(title='全国实时确诊数据',
                                            subtitle='数据来源：丁香园'),
                  legend_opts=opts.LegendOpts(is_show=False))
#render（）会生成本地 HTML 文件，默认会在当前目录生成 render.html 文件，也可以传入路径参数，如 m.render("mycharts.html")
m.render(path='/home/aistudio/data/饼状图.html')

结果图：
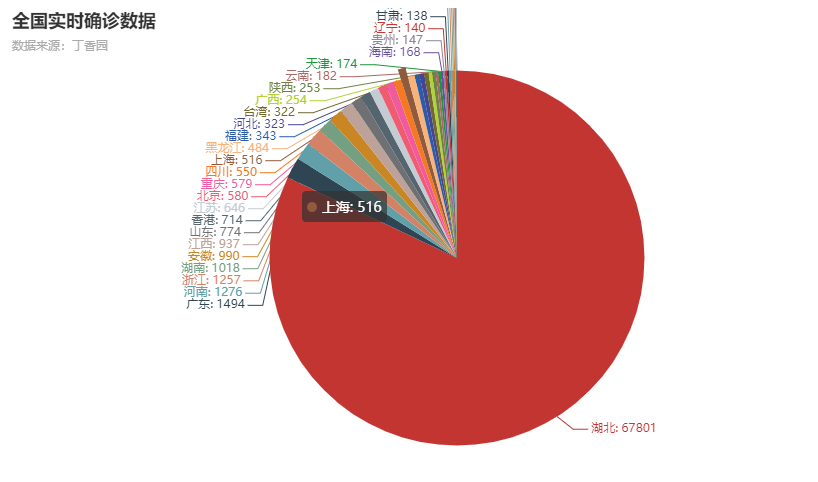
在这里插入图片描述

Day02手势识别

属于图像分类任务，根据图像的语义信息将不同类别图像区分开，是计算机视觉中重要的基本问题。手势识别属于图像分类中的一个细分类问题。
主要步骤：

  1. 准备数据
  2. 配置网络
  3. 训练网络
  4. 模型评估
  5. 模型预测
    定义的DNN全连接神经网络：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#定义DNN网络
class MyDNN(fluid.dygraph.Layer):
    def __init__(self):
        super(MyDNN,self).__init__()
        self.hidden1 = Linear(100,300,act="relu")
        self.hidden2 = Linear(300,500,act="relu")
        self.hidden3 = Linear(500,100,act="relu")
        self.hidden4 = Linear(3*100*100, 10, act="softmax")
    def forward(self,input):   
       x=self.hidden1(input) 
      #print(input.shape)
       x=self.hidden2(x)
       x=self.hidden3(x)
       x=fluid.layers.reshape(x,shape=[-1,3*100*100])
       #print(x.shape)
       y=self.hidden4(x)
       return y;

其中通过查看Paddle API，更改了几种不同的优化器和模型参数，最终accuracy还是达不到90%，还是不太会该如何选取参数。
识别结果：在这里插入图片描述

Day03-车牌识别

通过对经典的卷积网络模型比如LeNet的解析， 分为多个卷积层，激活层，池化层，然后是全连接层，最后通过Softmax函数将各分类标签通过概率表达出来。学会每一层的维度计算。
车牌识别中，需要事先将车牌中每个字符例如’沪’，’C’等切分出来，共形成65个分类，通过深度学习实际上最后预测的是车牌上的每个字符最大概率的预测字符，然后再拼接出来形成最终的识别结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#定义网络
class MyLeNet(fluid.dygraph.Layer):
    def __init__(self):
        super(MyLeNet,self).__init__()
        self.hidden1_1 = Conv2D(1,28,5,1)
        self.hidden1_2 = Pool2D(pool_size=2,pool_type='max',pool_stride=1)
        self.hidden2_1 = Conv2D(28,32,3,1)
        self.hidden2_2 = Pool2D(pool_size=2,pool_type='max',pool_stride=1)
        self.hidden3 = Conv2D(32,32,3,1)
        self.hidden4 = Linear(32*10*10,65,act='softmax')
    def forward(self,input):
        x=self.hidden1_1(input);
        x=self.hidden1_2(x);
        x=self.hidden2_1(x);
        x=self.hidden2_2(x);
        x=self.hidden3(x);
        x=fluid.layers.reshape(x,shape=[-1,32*10*10])
        y=self.hidden4(x);
        
        return y

Day04-口罩分类

检测在密集人流区域中戴口罩和未戴口罩的所有人脸，同时判断该人是否佩戴口罩。
vgg模型配置
在这里插入图片描述
vgg网络定义:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class VGGNet(fluid.dygraph.Layer):
    '''
    VGG网络
    '''
    def __init__(self):
        super(VGGNet, self).__init__()
        self.convpool01=ConvPool(3,64,3,2,2,2,act="relu")
        self.convpool02=ConvPool(64,128,3,2,2,2,act="relu")
        self.convpool03=ConvPool(128,256,3,2,2,3,act="relu")
        self.convpool04=ConvPool(256,512,3,2,2,3,act="relu")
        self.convpool05=ConvPool(512,512,3,2,2,3,act="relu")
        self.pool_5_shape=512*7*7
        self.fc01=fluid.dygraph.Linear(self.pool_5_shape,256,act="relu")
        self.fc02=fluid.dygraph.Linear(256,256,act="relu")
        self.fc03=fluid.dygraph.Linear(256,2,act="softmax")
 
    def forward(self, inputs, label=None):
        """前向计算"""
        #print(inputs.shape)
        x=self.convpool01(inputs)
        #print(x.shape)
        x=self.convpool02(x)
        #print(x.shape)
        x=self.convpool03(x)
        x=self.convpool04(x)
        x=self.convpool05(x)
        x=fluid.layers.reshape(x,shape=[-1,512*7*7])
        x=self.fc01(x)
        x=self.fc02(x)
        x=self.fc03(x)
        if label is not None:
            acc=fluid.layers.accuracy(input=x,label=label)
            return x, acc
        else:
            return x

人流密度检测问题

本竞赛所用训练和测试图片均来自一般监控场景，但包括多种视角（如低空、高空、鱼眼等），图中行人的相对尺寸也会有较大差异。部分训练数据参考了公开数据集（如ShanghaiTech [1], UCF-CC-50 [2], WorldExpo’10 [3]，Mall [4] 等）。

本竞赛的数据标注均在对应json文件中，每张训练图片的标注为以下两种方式之一：

（1）部分数据对图中行人提供了方框标注（boundingbox），格式为[x, y, w, h][x,y,w,h]；

（2）部分图对图中行人提供了头部的打点标注，坐标格式为[x, y][x,y]。

此外部分图片还提供了忽略区（ignore_region）标注，格式为[x_0, y_0, x_1, y_1, …, x_n, y_n]组成的多边形（注意一张图片可能有多个多边形忽略区），图片在忽略区内的部分不参与训练/测试。
人流密度检测网络训练使用的CNN模型网络配置如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

class CNN(fluid.dygraph.Layer):
    '''
    网络
    '''
    def __init__(self):
        super(CNN, self).__init__()

        
        self.conv01_1 = fluid.dygraph.Conv2D(num_channels=3, num_filters=64,filter_size=3,padding=1,act="relu")
        self.pool01=fluid.dygraph.Pool2D(pool_size=2,pool_type='max',pool_stride=2)

        self.conv02_1 = fluid.dygraph.Conv2D(num_channels=64, num_filters=128,filter_size=3, padding=1,act="relu")
        self.pool02=fluid.dygraph.Pool2D(pool_size=2,pool_type='max',pool_stride=2)

        self.conv03_1 = fluid.dygraph.Conv2D(num_channels=128, num_filters=256,filter_size=3, padding=1,act="relu")
        self.pool03=fluid.dygraph.Pool2D(pool_size=2,pool_type='max',pool_stride=2)

        self.conv04_1 = fluid.dygraph.Conv2D(num_channels=256, num_filters=512,filter_size=3, padding=1,act="relu")

        self.conv05_1 = fluid.dygraph.Conv2D(num_channels=512, num_filters=512,filter_size=3,padding=1, act="relu")
      

        self.conv06 = fluid.dygraph.Conv2D(num_channels=512,num_filters=256,filter_size=3,padding=1,act='relu')
        self.conv07 = fluid.dygraph.Conv2D(num_channels=256,num_filters=128,filter_size=3,padding=1,act='relu')
        self.conv08 = fluid.dygraph.Conv2D(num_channels=128,num_filters=64,filter_size=3,padding=1,act='relu')
        self.conv09 = fluid.dygraph.Conv2D(num_channels=64,num_filters=1,filter_size=1,padding=0,act=None)
        

    def forward(self, inputs, label=None):
        """前向计算"""
        out = self.conv01_1(inputs)
        
        out = self.pool01(out)

        out = self.conv02_1(out)
       
        out = self.pool02(out)
        out = fluid.layers.dropout(x=out,dropout_prob=0.25)
        out = self.conv03_1(out)
        
        out = self.pool03(out)
        out = fluid.layers.dropout(x=out,dropout_prob=0.25)
        out = self.conv04_1(out)    
        out = fluid.layers.dropout(x=out,dropout_prob=0.5)
        out = self.conv05_1(out)
        out = fluid.layers.dropout(x=out,dropout_prob=0.5)
        out = self.conv06(out)
        out = self.conv07(out)
        out = self.conv08(out)
        out = self.conv09(out)
        
        return out

通过几天的实践学习，掌握了训练的一般步骤，按照数据处理，配置网络，训练网络，模型评估和模型预测这样的步骤，再就是本地没GPU加速，运用百度paddle提供免费的算力，进行参数调优，但是对如何调整参数获得更好的效果，还是不太会。

发表于 更新于 分类于

Machine Learning(机器学习)是研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。

有一个算法叫支持向量机，里面有个巧妙的数学技巧，能让计算机处理无限多个特征。

监督学习：其基本思想是数据集中的每个样本都有相应的“正确答案”，再根据这些样本作出预测。例如垃圾邮件问题。
无监督学习：在无监督学习中，不同于监督学习的数据的样子（每条数据都有特定的标签，标明零件是正品还是次品），即无监督学习中没有任何的标签或者是有相同的标签或者就是没标签。
针对数据集，无监督学习就能判断出数据有两个不同的聚集簇，无监督学习算法可能会把这些数据分成两个不同的簇，所以叫做聚类算法。例如google新闻
聚类只是无监督学习中的一种，

损失函数（代价函数），也被称作平方误差函数，用J(θ_0,θ_1)表示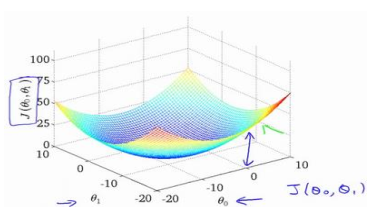
在这里插入图片描述
梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数
J(θ_0,θ_1)的最小值。
梯度下降背后的思想是：开始时我们随机选择一个参数的组合θ_0,θ_1,………….θ_n计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

同时更新是梯度下降中的一种常用方法。

假设你将θ_1初始化在局部最低点，结果是局部最优点的导数将等于零，新的θ_1等于原来的θ_1，如果参数已经处于局部最低点，那么梯度下降法更新其实什么都没做，它不会改变参数的值。这也解释了为什么即使学习速率α保持不变时，梯度下降也可以收敛到局部最低点。

线性回归算法：

在这里插入图片描述)在这里插入图片描述
在这里插入图片描述

开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

逻辑回归：

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

逻辑回归的代价函数：

在这里插入图片描述
根据这个代价函数，为了拟合出参数，我们要找出让J(θ)取得最小值的参数θ
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述)在这里插入图片描述
线性回归和逻辑回归更新参数的规则看起来基本相同，但由于假设的定义发生了变化，所以逻辑函数的梯度下降，跟线性回归的梯度下降实际上是两个完全不同的东西。
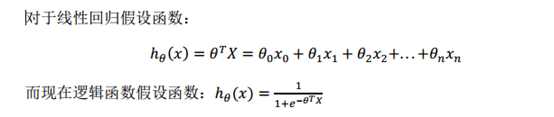
在这里插入图片描述

过拟合问题

线性回归和逻辑回归，它们能够有效地解决许多问题，但是当将它们应用到某些特定的机器学习应用时，会遇到过拟合(over-fitting)的问题，可能会导致它们效果很差，正则化技术可以改善或者减少过度拟合问题。
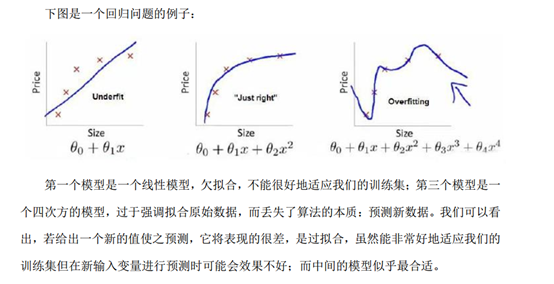
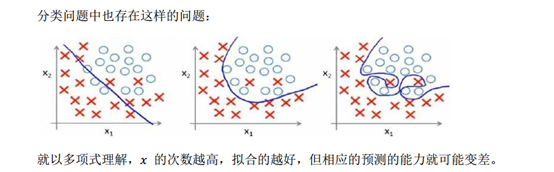
在这里插入图片描述
在这里插入图片描述

过拟合问题的处理：1.丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如PCA）
2.正则化。 保留所有的特征，但是减少参数的大小（magnitude）

回归问题中我们的模型是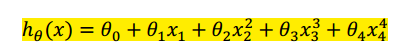：在这里插入图片描述
正是这些高次项导致了过拟合的产生，所以如果我们能让这些高次项的系数接近于 0 的话，就能很好的拟合了。
我们要做的就是在一定程度上减小这些参数θ的值，这就是正则化的基本方法。

特征的直观理解：
从本质上讲，神经网络能够通过学习得出其自身的一系列特征。在普通的 逻辑回归中，我们被限制为使用数据中的原始特征${x_1},{x_2}, \ldots ,{x_n}$，我们虽然可以使用一些二项式项来组合这些特征，但是我们仍然受到这些原始特征的限制。
在神经网络中，原始特征只是输入层，在我们上面三层的神经网络例子中，第三层也就是输出层做出的预测利用的是第二层的特征，而非输入层中的原始特征，我们可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征。

反向传播算法

为了计算代价函数的偏导数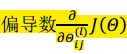在这里插入图片描述 ，我们需要采用一种反向传播算法，首先计算最后一层的误差，然后再一层一层反向求出各层的误差，直到倒数第二层。

使用神经网络时候的步骤：

网络结构：第一件要做的事是选择网络结构，即决定选择多少层以及决定每层分别有多
少个单元。
第一层的单元数即我们训练集的特征数量。
最后一层的单元数是我们训练集的结果的类的数量。
如果隐藏层数大于 1，确保每个隐藏层的单元个数相同，通常情况下隐藏层单元的个数
越多越好。我们真正要决定的是隐藏层的层数和每个中间层的单元数。
训练神经网络：

  1. 参数的随机初始化
  2. 利用正向传播方法计算所有的h_θ (x)
  3. 编写计算代价函数J的代码
  4. 利用反向传播方法计算所有偏导数
  5. 利用数值检验方法检验这些偏导数
  6. 使用优化算法来最小化代价函数

    应用机器学习，决定下一步该做什么

　　      在开发一个机器学习系统，或者想试着改进一个机器学习系统的性能，应该如何决定接下来应该选择哪条道路？
　　为了解释这一问题，我想仍然使用预测房价的学习例子，假如你已经完成了正则化线性回归，也就是最小化代价函数。一种办法是使用更多的训练样本，另一个方法是尝试选用更少的特征集。
　　当我们运用训练好了的模型来预测未知数据的时候发现有较大的误差，我们下一步可以做什么？ 通常获得更多的训练实例是有效的，但代价较大。

考虑采用下面的方法:
1.尝试减少特征的数量
2.尝试获得更多的特征
3.尝试增加多项式特征
4.尝试减少正则化程度λ
5.尝试增加正则化程度λ
当你运行一个学习算法时，如果这个算法的表现不理想，那么多半是出现两种情况：要么是偏差比较大，要么是方差比较大。换句话说，出现的情况要么是欠拟合，要么是过拟合问题。
将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来分析：
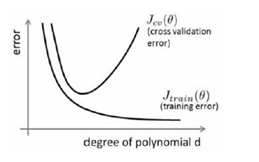
在这里插入图片描述
上面的曲线是交叉验证集，下面的曲线是训练集。
对于训练集，当d较小时，模型拟合程度更低，误差较大；随着d的增长，拟合程度提高，误差减小。
对于交叉验证集，当d较小时，模型拟合程度低，误差较大；但是随着d的增长，误差呈现先减小后增大的趋势，转折点是我们的模型开始过拟合训练数据集的时候。
在这里插入图片描述
训练集误差和交叉验证集误差近似时：偏差/欠拟合
交叉验证集误差远大于训练集误差时：方差/过拟合

正则化和偏差、方差

在我们在训练模型的过程中，一般会使用一些正则化方法来防止过拟合。但是我们可能
会正则化的程度太高或太小了，选择 λ 的值时也需要思考这些问题。

将训练集和交叉验证集模型的代价函数误差与 λ 的值绘制在一张图表上：
在这里插入图片描述
当λ较小时，训练集误差较小（过拟合）而交叉验证集误差较大；
随着λ的增加，训练集误差不断增加（欠拟合），而交叉验证集误差则是先减小后
增加。

学习曲线

学习曲线是一种很好的工具，可以用来判断某一个学习算法是否处于偏差、方差问题。学习曲线是学习算法的一个很好的合理检验。
学习曲线是将训练集误差和交叉验证集误差作为训练集实例数量（m）的函数绘制的图表

逻辑回归算法是分类算法

适用于标签Y取值离散的情况，如1001。

梯度下降算法的每次迭代受到学习率的影响，如果学习率α过小，则达到收敛所需的迭
代次数会非常高；如果学习率α过大，每次迭代可能不会减小代价函数，可能会越过局部最
小值导致无法收敛。

泛化能力

泛化能力就是模型对未知数据的预测能力。在实际当中，我们通常通过测试误差来评价学习方法的泛化能力。

机器学习中训练集、交叉验证集、测试集的理解

训练集（train set） —— 用于模型拟合的数据样本。
验证集（development set）—— 是模型训练过程中单独留出的样本集，它可以用于调整模型的超参数和用于对模型的能力进行初步评估。
在神经网络中， 我们用验证数据集去寻找最优的网络深度（number of hidden layers)，或者决定反向传播算法的停止点或者在神经网络中选择隐藏层神经元的数量；
在普通的机器学习中常用的交叉验证（Cross Validation) 就是把训练数据集本身再细分成不同的验证数据集去训练模型。
测试集 —— 用来评估模最终模型的泛化能力。但不能作为调参、选择特征等算法相关的选择的依据。
在这里插入图片描述
关于训练集、验证集、测试集的一个形象的比喻：

训练集-----------学生的课本；学生 根据课本里的内容来掌握知识。

验证集------------作业，通过作业可以知道 不同学生学习情况、进步的速度快慢。

测试集-----------考试，考的题是平常都没有见过，考察学生举一反三的能力。

传统上，一般三者切分的比例是：6：2：2，验证集并不是必须的

误差分析

构建一个学习算法的推荐方法为：

  1. 从一个简单的能快速实现的算法开始，实现该算法并用交叉验证集数据测试这个算法
  2. 绘制学习曲线，决定是增加更多数据，或者添加更多特征，还是其他选择
  3. 进行误差分析：人工检查交叉验证集中我们算法中产生预测误差的实例，看看这些实例
    是否有某种系统化的趋势
    ==推荐在交叉验证集上来实施误差分析，而不是在测试集上。==

单变量线性回归问题：
全局最小点是局部下降算法的最大点，
SVM（支持向量机）、奇异值分解。

SVM

SVM的全称是Support Vector Machine，即支持向量机，主要用于解决模式识别领域中的数据分类问题，属于有监督学习算法的一种。SVM要解决的问题可以用一个经典的二分类问题加以描述。

线性回归

在这里插入图片描述
主要是拟合一条直线，使尽可能多的点落在直线上。

逻辑回归

逻辑回归虽然名字叫做回归，但实际上却是一种分类学习方法。 线性回归完成的是回归拟合任务，而对于分类任务，我们同样需要一条线，但不是去拟合每个数据点，而是把不同类别的样本区分开来。
bagging是一种用来提高学习算法准确度的方法

决策树

https://blog.csdn.net/jiaoyangwm/article/details/79525237

决策树与随机森林都属于机器学习中监督学习的范畴，主要用于分类问题。

决策树算法有这几种：ID3、C4.5、CART，基于决策树的算法有bagging、随机森林、GBDT等。决策树是一种利用树形结构进行决策的算法，对于样本数据根据已知条件或叫特征进行分叉，最终建立一棵树，树的叶子结节标识最终决策。新来的数据便可以根据这棵树进行判断。随机森林是一种通过多棵决策树进行优化决策的算法。

SVM是否属于神经网络

参考链接
在这里插入图片描述
SVM效果很大程度依赖kernel的设计
具体地说，线性SVM的计算部分和一个单层神经网络一样，就是一个矩阵乘积。SVM的关键在于它的Hinge Loss以及maximum margin的想法。其实这个loss也是可以用在神经网络里的（参见object detection的R-CNN方法）。对于处理非线性数据，SVM和神经网络走了两条不同的道路：神经网络通过多个隐层的方法来实现非线性的函数，有一些理论支持（比如说带隐层的神经网络可以模拟任何函数），但是目前而言还不是非常完备；SVM则采用了kernel trick的方法，这个在理论上面比较完备（RKHS，简单地说就是一个泛函的线性空间）。两者各有好坏，神经网络最近的好处是网络设计可以很灵活，但是老被人说跳大神；SVM的理论的确漂亮，但是kernel设计不是那么容易，所以最近没有那么热了。

发表于 更新于 分类于

利用keras实现手写数字辨识

首先要建一个Network scratch，input是28∗28的dimension，其实就是说这是一张image，image的解析度是28∗28，把它拉成长度是28∗28维的向量。output呢？现在做的是手写数字辨识，所以要决定它是0-9的哪个数字，output就是每一维对应的数字，所以output就是10维。中间假设你要两个layer，每个layer有500个hidden neuro

创建一个network

1
model=Sequential()

添加第一个hidden layer, 　Dense意思为添加一个全连接网络，Ｃon2d表示添加一个convolution layer卷积层，input_dim表示输入维度，units表示hidden layer的神经元个数，activation表示激活函数，可以为relu，sigmoid，tanh，softmax，hard_sigmoid，linear等

1
model.add(Dense(input_dim=28*28,units=500,activation='relu'))

再添加一个layer

1
model.add(Dense(units=500,activation='relu'))

最后的输出层，由于是数字识别一共10个数字，所以output是10维，units=10,激活函数选择softmax

1
model.add(Dense(units=10,activation='softmax'))

configuration配置

　　需要定义loss function，选择optimizer，以及评估指标metrics，其实所有的optimizer都是Gradent descent based，只是有不同的方法来决定learning rate，比如Adam，SGD，RMSprop，Adagrad，Adalta，Adamax ，Nadam等，configuration完成之后就可以开始train创建的Network。

1
model.compile(loss='categorical crossentropy',optimizer='adam',metrics=['accuracy'])

pick the best function

model.fit方法，开始用Gradent Descent帮你去train你的Network，那么你要给它你的train_data input 和label，这里x_train代表image，y_train代表image的label，关于x_train和y_train的格式，你都要存成numpy array。

1
model.fit(x_train,y_train,batch_size=100,epochs=20)

使用模型

接下来要拿train的network来使用，使用有两个不同的情景，这两个不同的情景一个是evaluation，意思就是说你的model在test data 上到底表现得怎样，call evaluate这个函数，然后把x_test，y_test喂给它，就会自动给你计算出Accuracy。它会output一个二维的向量，第一个维度代表了在test set上loss，第二个维度代表了在test set上的accuracy，这两个值是不一样的。loss可能用cross_entropy，Accuraccy是对与不对，即正确率。

  • case 1
    1
    2
    3
    score = model.evaluate(x_test,y_test)
    print('Total loss on Testiong Set : ',score[0])
    print('Accuracy of Testiong Set : ',score[1])
    第二种是做predict，就是系统上线后，没有正确答案的，call predict进行预测
  • case 2
    1
    result = model.predict(x_test)

    快速理解epoch、iteration和batch

    假设有1000个训练样本，batch_size=20,则iteration就是50，将所有的训练样本在同一个模型中训练5遍
    batch_size * iteration = 样本数量，epoch=5.
    所有样本完成一次前向传播+反向传播为一个epoch

    batchsize：简单点说，就是我们一次要将多少个数据扔进模型去训练，这个值介于1和训练样本总个数之间。
    iteration：迭代的次数（向模型中扔数据的次数）,一个迭代= 同一批batchsize数据的一个正向通过+一个反向通过。
    Epoch: 训练集中的全部样本都在训练模型中走了一遍，并返回一次（有去有回），为一个epoch。

由于这个例子中需要使用MNIST数据集，给出的源码中使用(x_train, y_train), (x_test, y_test) = mnist.load_data() 下载数据集，但是过程中需要翻墙，故我在此先将MNIST数据集的包下载下来，然后稍微修改下代码，完成数据的import.其中，numpy.load() 函数可以读取 .npy .npz 等文件类型，并返回对应的数据类型。
1）如果文件类型是 .pny 则返回一个1维数组。
2）如果文件类型是 .npz 则返回一个类似字典的数据类型，包含 {filename: array} 键值对。

1
2
3
4
5
path = 'C:\\Users\\Administrator\\Desktop\\mnist.npz'
    f = np.load(path)
    x_train, y_train = f['x_train'], f['y_train']
    x_test, y_test = f['x_test'], f['y_test']
    f.close()

下载地址：mnist数据集
提取码：gyt8

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import numpy as np
from keras.models import Sequential
from keras.layers.core import Dense,Dropout,Activation
from keras.optimizers import SGD,Adam
from keras.utils import np_utils
from keras.datasets import mnist

def load_data():
    path = 'C:\\Users\\Administrator\\Desktop\\mnist.npz'
    f = np.load(path)
    x_train, y_train = f['x_train'], f['y_train']
    x_test, y_test = f['x_test'], f['y_test']
    f.close()
    number=10000
    x_train=x_train[0:number]
    y_train=y_train[0:number]
    x_train=x_train.reshape(number,28*28)
    x_test=x_test.reshape(x_test.shape[0],28*28)
    x_train=x_train.astype('float32')
    x_test=x_test.astype('float32')
    y_train=np_utils.to_categorical(y_train,10)
    y_test=np_utils.to_categorical(y_test,10)
    x_train=x_train
    x_test=x_test
    x_train=x_train/255
    x_test=x_test/255
    return (x_train,y_train),(x_test,y_test)

(x_train,y_train),(x_test,y_test)=load_data() #载入数据

model=Sequential()
model.add(Dense(input_dim=28*28,units=633,activation='sigmoid')) #维度28*28，激活函数为sigmoid
model.add(Dense(units=633,activation='sigmoid'))
model.add(Dense(units=633,activation='sigmoid'))
for i in range(10):
	model.add(Dense(units=689,activation='sigmoid'))
	
model.add(Dense(units=10,activation='softmax')) #输出层一定要是10维，units=10;

model.compile(loss='mse',optimizer=SGD(lr=0.1),metrics=['accuracy'])  #config

model.fit(x_train,y_train,batch_size=100,epochs=20)

result= model.evaluate(x_test,y_test)

print('\nTEST ACC:',result[1])

添加10层，发现结果还是11%的accuracy
在这里插入图片描述
首先先看你在train data的performer，如果它在train data上做得好，那么可能是过拟合，如果在train data上做得不好，怎么能让它做到举一反三呢。所以至少先让它在train data 上得到好的结果。
在这里插入图片描述)在这里插入图片描述
由得到的结果发现train data acc 也是差的，就说明train没有train好，并不是overfiting过拟合。
接下来进行调参过程:
MSE均方误差不适合于分类问题，将loss function改为categorical_crossentropy，看看结果如何：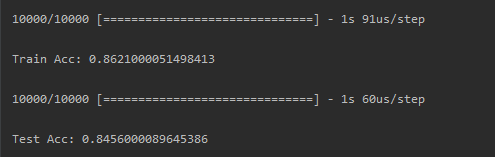
在这里插入图片描述
发现一换成交叉熵categorical_crossentropy，在train set上的结果就变得很好了。得到86.21%的正确率。

activation function

把sigmoid都改为relu，发现在train的accuracy就爬起来了，train的acc已经将近100分了，test 上也可以得到95.45%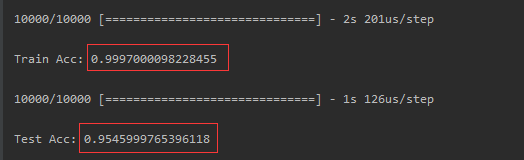
在这里插入图片描述

发表于 更新于 分类于

面试题04. 二维数组中的查找

问题描述

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

现有矩阵 matrix 如下：

[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。
给定 target = 20，返回false。

阅读全文 »

发表于 更新于 分类于

面试题03. 数组中重复的数字

本题要求找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例1：

输入： [2,3,1,0,2,5,3]

输出： 2或3

限制：2 <= n <= 100000

阅读全文 »

发表于 更新于

找到Anaconda的安装目录
在这里插入图片描述

使用cmd命令打开终端
然后输入

1
python .\Lib_nsis.py mkmenus

在这里插入图片描述
完美解决问题。
在这里插入图片描述
在这里插入图片描述